编译原理Ch1

第一章 引论 && 第二章

1.1 编译程序（Compiler）

可变目标编译程序

交叉编译程序

1.2 编译程序的组成

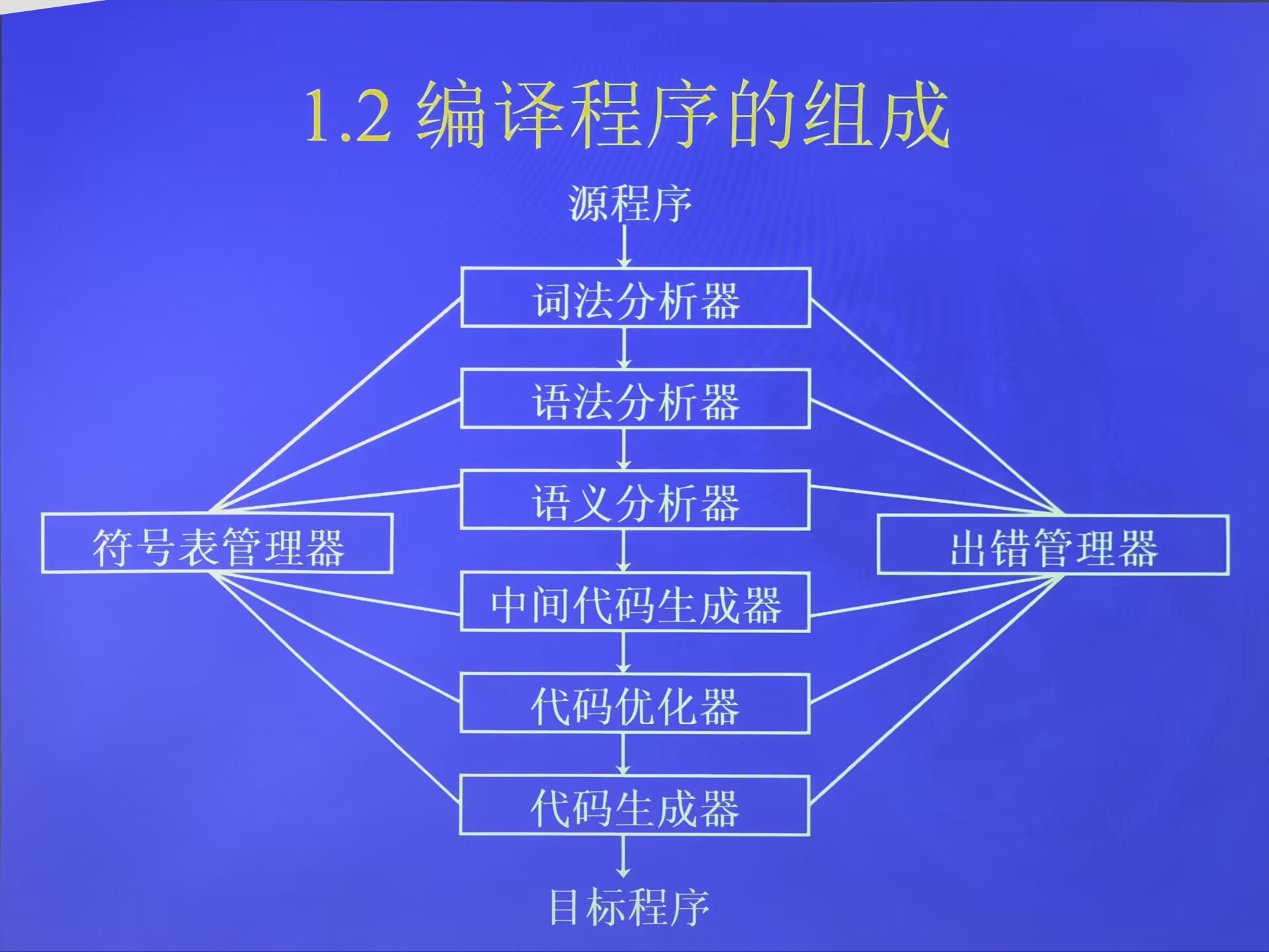
1.2.1（第二重要）词法的：lexical

• 将你输入的代码转化成一个个单词（当你写完代码后，你的程序代码相当于一个大长字符串）

1.2.2（最重要）语法分析器：按照语法分析程序结构，结构决定功能※

程序包括:

• 返回类型：int
• 标识符：main
• 参数表：(
• 参数序列：)
• 函数体：{语句;}

1.2.3 语义分析：不重要，知道就行

1.2.4（第三重要）中间代码生成：将你的代码转化为所谓的中间代码

源代码有m个源程序，n个目标平台，如果有中间代码，那么程序员的工作量是$m+n$；如果没有，工作量是$m*n$

1.2.5 代码优化器：不重要，知道就行

1.2.6 代码生成器：不重要，知道就行

编译器只是给什么就干什么，不知道整体程序要干什么，程序是由这个过程的线性序列组成的

1.2.7 三个概念

• 前端：前四个

• 后端：后二个

• 遍：编译器一遍扫描，完成自己的工作

1.3 高级语言及其语法特征

1.3.1 程序语言的语法和语义

语言：

• 定义在某个字母表上的句子的集合（自然语言/程序语言）
• 自然语言的定义是不断变化的，程序设计语言的结构定义是固定的
• 语法：
  

语义：

• 定义程序的意义。没有公认的形式系统描述语义

高级语言的分类：不重要，与编译器的关联都在语义层面

• 强制式语言/过程式语言/命令式语言：FORTRAN,C,Pascal
• 应用式/函数式语言：LISP
• 基于规则的语言：Prolog
• OO的语言：

1.3.2 程序语言的语法描述

字母表和符号串

• 例：C的字母表：ASCII
• 例：C#：UNICODE
• 序列：线性生成符号串，无法出现乘方/积分/∑类似的方式

符号串和符号串集合的运算

• 相等：
• 长度：$|e|=0$
• 连接：拼一起。(ex=xe)
• 符号串集合的乘积运算
  
• 幂运算
  • $for∈∑^3$
  • $while∈∑^5$
  • $main∈∑^4$
• 闭包运算
  • 正则闭包：$∑^+=∑^1∪∑^2∪…∪∑^n∪…$
  • 闭包：$∑^*=∑^0∪∑^+$

1.3.3 文法的直观理解

什么是文法

• 文法是对语言结构的定义与描述。即从形式上用于描述和规定语言结构的称为“文法”（或称为“语法”）。

语法规则

• 我们通过建立一组规则（产生式），来描述句子的语法结构。规定用“::=”表示“由……组成”。
  

由产生式推导句子

• 有了一组产生式之后，可以按照一定的方式用它们去推导或产生句子。
• 推导方法：从一个要识别的符号开始推导，即用相应产生式的右部来替代产生式的左部，每次仅用一条产生式去进行推导。

  例：
  <句子> => <主语><谓语>
  <主语><谓语> => <代词><谓语> …
  这种推导一直进行下去，直到所有带< >的符号都由终结符号替代为止。

语法树

• 我们用语法树来描述一个句子的语法结构。
  

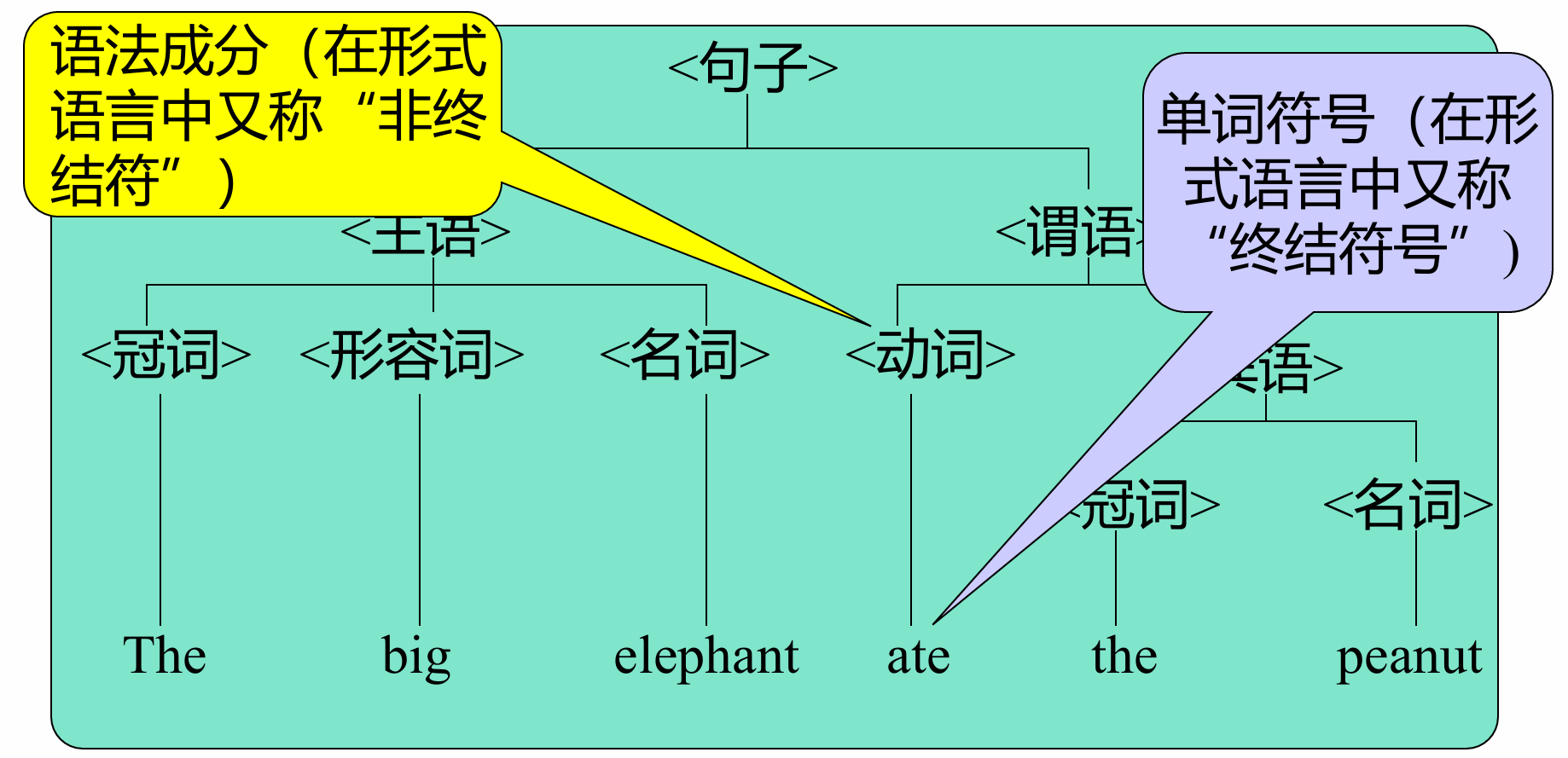
1.3.4 文法和语言的形式定义

文法的定义

定义（乔姆斯基）：文法$G=(V_N,V_T,P,Z)$

• $V_N$：非终结符号集
• $V_T$：终结符号集
• $P$：产生式或规则的集合
• $Z$：开始符号（识别符号）$Z∈{V_N}$

人话：终结符是不可拆分的，非终结符可以被拆分为终结符或非终结符，产生式就是非终结符拆分的规则/过程，开始符号是最开始那个产生式的左部

推导与规约

• 直接推导：
  

  换句话说，x和y是符号串，若使用一次产生式可以从x变换出y，则称x直接推导出y（或者说y是x的直接推导），记为$x⇒y$

• +推导：x和y是符号串，若使用若干次（大于0）产生式可以从x变换出y，则称x推导出y（或者说y是x的推导），记为$A \overset{+}{\Rightarrow} B$
• *推导：x和y是符号串，若使用0次或若干次产生式可以从x变换出y，则称x*推导出y（或者说y是x的*推导），记为$A \overset{*}{\Rightarrow} B$
• 最右推导：若符号串α中有两个以上的非终结符时，对推导的每一步坚持把α中的最右非终结符进行替换，称为最右推导。
• 最左推导：若符号串α中有两个以上的非终结符时，对推导的每一步坚持把α中的最左非终结符进行替换，称为最左推导。
• 规约：推导的逆过程

语言的形式定义

对于文法G[Z]:

• 句型：x是句型 $ \Leftrightarrow $ $ \space Z \overset{*}{\Rightarrow} x$，且$x∈V^{\ast}$;

• 句子：x是句子 $ \Leftrightarrow $ $\space Z \overset{+}{\Rightarrow} x$，且$x∈{V^*_T}$;

• 语言：$L(G[N])$= { $ x|\space Z \overset{+}{\Rightarrow} x，x∈{V^*_T} $ }

  例：
  
  等价文法：G和G`是不同文法，若L(G)=L(G`)，则二者是等价文法

文法分类

• 形式语言：用文法和自动机所描述的没有意义的语言
• 0型文法： $ P: u \rightarrow v，其中u∈V^+，v∈V^*$

人话：产生式左边有符号（非空），右边随意

• 1型文法：$ P: xUy\rightarrow xuy，其中U∈V_N，x、y、u∈V^*$

  人话：0型基础上，有非终结符

• 2型文法(※)：$P：U\rightarrow u，其中U∈V_N，u∈{V^*}$

  人话：1型基础上，产生式左部只有一个符号且是非终结符（另：上下文无关）

• 3型文法(※)：
  • （左线性）$P：U\rightarrow T或U\rightarrow wT，其中U、w∈V_N，T∈V_T$
  • （右线性）$P：U\rightarrow T或U\rightarrow Tw，其中U、w∈V_N，T∈V_T$

    人话：右边要么没有非终结符，要么只有一个

语法树与二义性文法

• 若对于一个文法的某一句子存在两棵不同的语法树，则该文法是二义性文法，否则是无二义性文法。
• 若一个文法的某句子存在两个不同的规范推导，则该文法是二义性的，否则是无二义性的。