编译原理Ch3

第三章 词法分析

一、手工构造词法分析器

1.词法分析器的功能和输出形式

功能：输入源程序，输出单词符号

单词符号：一个程序语言的基本语法符号

单词分类（5类）：

• 关键字：由程序语言定义的具有固定意义的标识符。也称为保留字或基本字。
• 标识符：用来表示程序中各种名字的字符串
• 常数：整型、实型、布尔型、文字型
• 运算符：+、-、*、/
• 界限符：逗号，分号，括号等

二、正则表达式与有限自动机

1.正规式与正规集

(1)正规式也称正则表达式

(2)正规表达式（regular expression）

• 是说明单词的模式（pattern）的一种重要的表示法（记号），是定义正规集的一种重要的数学工具。

(3)定义（正规式和它所表示的正规集）：

设字母表为∑，辅助字母表 Σ`= { $\varepsilon,\varphi, |,·,*,(,)$ }

• $ \varepsilon,\varphi $都是正规式，表示的正规集是{ $ \varepsilon $ },{ $ \varphi $ }
• 对任意a∈∑，a是正规式，表示的正规集是{a}
• $ e_1、e_2$是正规式，表示的正规集是$L(e_1)$、$L(e_2)$，则$(e_1)$、$e_1|e_2$、$e_1·e_2$、$e^*$也是正规式，表示的正规集分别为$L(e_1)$、$L(e_1)$∪$L(e_2)$、$L(e_1)$ $L(e_2)$和$(L(e_1))^*$

(4)正规式的等价性

• 若两个正规式的正规集相等，那么正规式等价，记作$e_1=e_2$

2.确定有限自动机

(1)DFA定义：

一个确定的有穷自动机（DFA）M是一个五元组M=（S，Σ，δ，$s_0$，F），其中

• S是一个有穷集，它的每一个元素称为一个状态
• Σ是一个有穷字母表，它的每个元素称为一个输入符号，所以也称Σ为输入符号表
• δ是转换函数，是在S×Σ→S上的单值部分映射，即，如果 δ（s，a）=s’，（s∈S，s’∈S）就意味着，当前状态为s，输入符为a时，将转换为下一个状态s’，s’称作s的一个后继状态
• $s_0$ ∈S是唯一的一个初态
• F ⊂ S是一个终态集（可空），终态也称可接受状态或结束状态
  

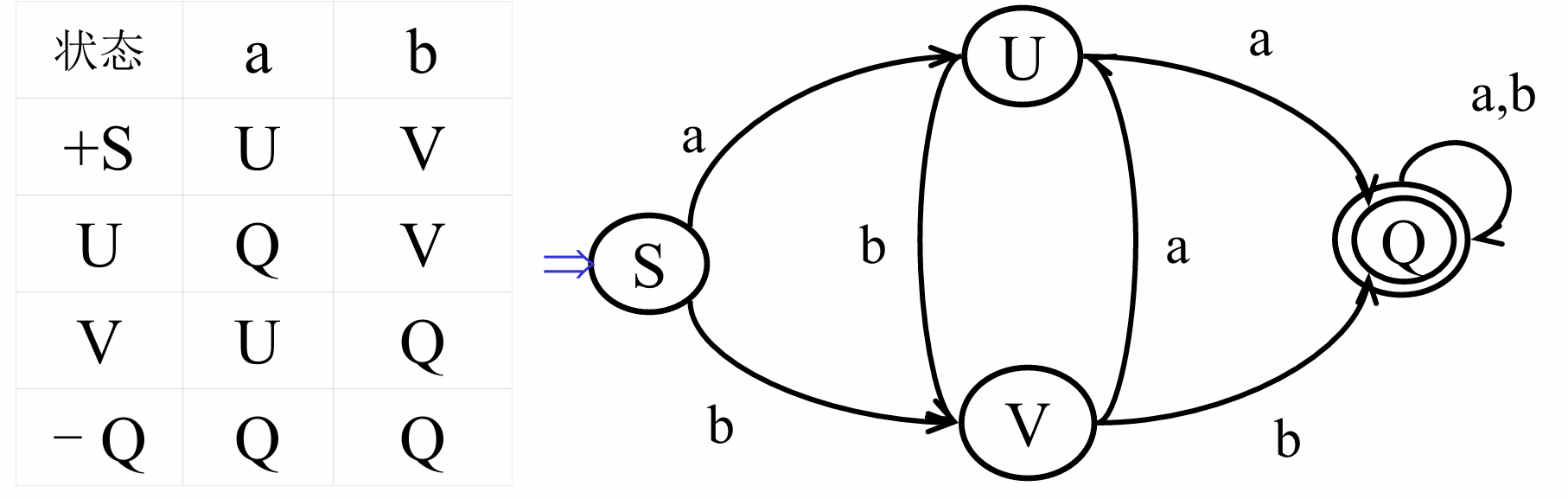
  给定e∈Σ，若e中的每个字母可以沿着DFA的图从起始状态到终止状态，则e被DFA M所识别（接受），否则为不接受。例：e=abb可被识别

3.非确定的有穷自动机NFA

(1)定义；

一个非确定的有穷自动机（NFA）M是一个五元组：$M=（S，Σ， δ，S_0，F）$,其中:

• S是一个有穷集，它的每个元素称为一个状态；
• Σ是一个有穷字母表，它的每个元素称为一个输入符号，所以也称Σ为输入符号表；
• δ是状态转换函数，是在S×Σ*→S的子集的映射，即， $δ : S×Σ^*→2^S $；表明在某状态下对于某输入符号可能有多个后继状态；
• $S_0 ⊂ S$是一个非空初态集；
• $F ⊂ K$是一个终态集（可空）。

三、NFA确定化（NFA→DFA）

1.列表，第一行是初态，通过各个字母到达其他状态

2.求其他状态的$\varepsilon$闭包

3.将最左边一列没出现过的状态重复1和2

4.画图，初态是原来的初态，终态为包含原来终态的所有状态

四、DFA最小化

1.将状态集合划分为两个集合，非终态集和终态集

2.将非终态集继续划分

• 根据字母表中的每个元素，一一代入状态转换函数中，将接收和不接受的集合分开
• 重复这个步骤，最终将状态集划分为多个集合，这几个集合组成的集合为

$P=$ { $S_1，S_2，…，S_i$ }

3.在P的每个元素中选出一个代表，将相同组的状态元素全部替换。

把原来导入非代表状态的弧均导入其代表即可，即若$k^′$是一代表且$f(k^′,a)=t$,令$r$是$t$组的代表，则$M^′$中有一转换$f^′(k^′,a)=r$，$M^′$的开始状态是含有$S_0$的那组的代表，$M^′$的终态是含有$F$的那组的代表。

五、正规式转化为NFA

1.转化方法

将正规式的每个元素一步一步按照规则进行转化

2.规则

(1)$e_1·e_2$

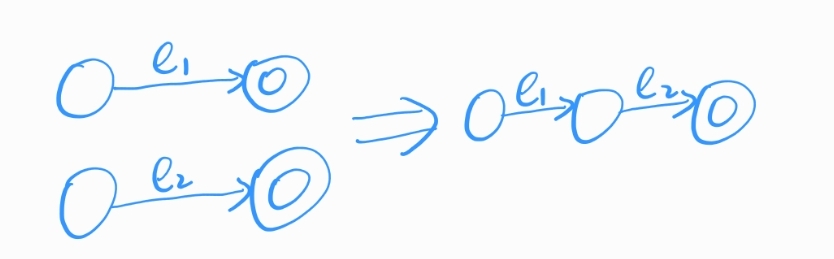
(2)$e^*$

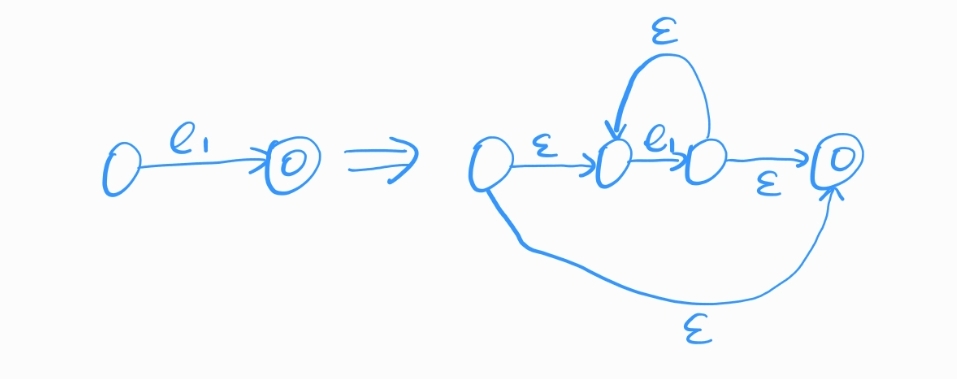
(3)$e_1|e_2$

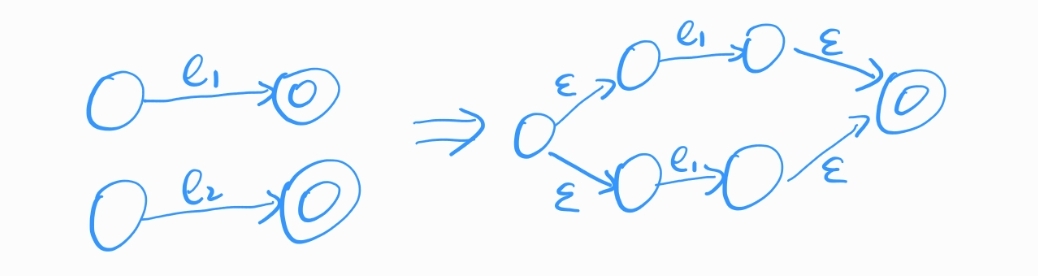
六、把给定的∑上的NFA M转换为一个正规文法G[R]的构造规则:

设$NFA \space\space M=（ K，Σ，f，S，Z），G[R]=（V_N，V_T，P，R）$

1.令$V_T=Σ$

正规文法的终结符集就是NFA的字母表

2.令$V_N=K$

即对M的每个状态生成非终结符（不妨取相同名字，G的开始符号是M的初态）

3.令$S=R$

如果M有多个初态，应先拓广自动机，引入新初态x；
方法：选定一个初态，与其他初态之间用$\varepsilon$弧连接

4.对M增加一个产生式：$Z→\varepsilon$

终态推导出$\varepsilon$

5.构造G的产生式

对M中的每个状态转换函数$δ(A,t)=B$得出G的一个产生式$A→tB$（t为终结符或$\varepsilon$，A、B为非终结符）