编译原理Ch4
第四章 自顶向下语法分析方法
一、三种集合定义
1.首符集
设$G=(V_N ,V_T,P,S)$是上下文无关文法,$α$是$G$的任一符号串,则有:
$FIRST(α)= ${$ a|α\overset*{\Rightarrow}aβ,a∈V_T,α、β∈V^*$}
特别地,若$α\overset{*}{\Rightarrow} \varepsilon$,则$\varepsilon∈FIRST(α)$
即: FIRST(α)是从α出发推导出的所有符号串首终结符或可能的ε构成的集合。
2.后继符集
设$G=(V_N ,V_T,P,S)$是上下文无关文法,$A∈V_N$的后继符集合为:
$FOLLOW(A)=${$a|S \overset*{\Rightarrow} μAβ且a∈V_T ,a∈ FIRST(β),μ∈{V_T}^*,β∈V^*$}
或者
$FOLLOW(A)=${$a | S \overset*{\Rightarrow} …Aa… ,a∈V_T$}
特别地,若$S \overset{*}{\Rightarrow} …A$,则#$∈FOLLOW(A)$
3.选择集
对于给出上下文无关文法的产生式$A→α,A∈V_N,α∈V^*$,则
$$SELECT(A→α)= \begin{cases} FIRST(α), & \text {否则} \\ FIRST(α)∪FOLLOW(A), & α\overset{*}{\Rightarrow} \varepsilon\end{cases}$$
二、三种集合的构造算法
1.求FIRST(X)的算法
对每一文法符号$X∈(V_N∪V_T)$,求$FIRST(X)$
(1)若$X∈V_T$,则令$FIRST(X)=${$X$}
(2)若$X∈V_N$,且有产生式X→a…($a∈V_T$)(右部终结符打头),则令$a∈FIRST(X)$
(3)若$X∈V_N$,有$X→\varepsilon$,则令$\varepsilon∈FIRST(X)$
(4)若$X∈V_N,y_1,y_2,…,y_i∈V_N$,且有产生式$X→ y_1 y_2…..y_n$,当$y_1, y_2,…,y_{i-1}都\overset{*}{\Rightarrow} \varepsilon$,(其中1≤i≤n),则$FIRST(y_1)-ε$,$FIRST(y_2)-ε$,…,$FIRST(y_{i-1})-ε$,$FIRST(y_i)$都加到$FIRST(X)$中
(5)当(4)中所有$y_i\overset{*}{\Rightarrow} \varepsilon \space i=(1,2,3,…,n)$则$FIRST(X)=FIRST(y_1)∪FIRST(y_2)∪…∪FIRST(y_n)∪ {ε}$
(6)反复使用上述(2)~(4) 步直到每个符号的FIRST集合不再增加为止。
2.求FOLLOW(A)的算法$(A∈V_N)$
(1)“落#下S” 对文法开始符号S,令#$∈FOLLOW(S)$
(2)“右部FOLLOW” 若$B→αAβ$是一个产生式,则令$FIRST(β)-${$ε$}属于$FOLLOW(A)$
(3)“守门员福利” 若$B→αA$是一个产生式,或$B→αAβ$是一个产生式且有$ε∈FIRST(β)$,则令$FOLLOW(B)$是$FOLLOW(A)$的子集。即把$FOLLOW(B)$的所有元素加入到$FOLLOW(A)$中。
(4)反复使用(2)直到每个非终结符的FOLLOW集合不再增加为止。
3.求SELECT(A→α)的算法(使用SELECT定义)
(1)求$FIRST(α)$
(2)若$ε∉FIRST(α)$,则令$SELECT(A→α)=FIRST(α)$,否则求$FOLLOW(A)$,并令$SELECT(A→α)=FIRST(α) ∪ FOLLOW(A)$
三、LL(1)分析法
1.定义:
- 一个上下文无关文法是LL(1)文法的充分必要条件是每个非终结符A的两个不同产生式,$A→α ,A→β$;满足$SELECT(A →α ) ∩ SELECT(A →β)= Ф$。其中α、β不能同时 $\overset{*} {\Rightarrow} \varepsilon$。
二、文法的等价交换
1.提取公共左因子
若文法中含有形如:$Α→αβ|αγ$的产生式,这导致了对相同的产生式右部的FIRST集相交。
即有$SELECT(A→ αβ)SELECT(A→ αγ)≠φ$。
不满足$LL(1)$文法的充要条件。等价交换为:
$A→ αA’$和 $A’→ β| γ$
2.消除左递归
当一个文法含有下列形式的产生式之一时:
- $A→Aβ,A∈V_N,β∈V^*$
- $A→Bβ,B→A α,A,B∈V_N,α,β∈V^*$
则称该文法是左递归的。
含有左递归的文法不能采取自顶向下分析法。
方法:把左递归改写为右递归:
三、递归下降分析程序构造
1.每个非终结符对应一个过程(函数、方法)
2.根据产生式生成每一个过程的内容
3.例子


四、预测分析程序
1.验证是否为LL(1)文法
2.构造预测分析表
- 构造方法:若$SELECT(A→B)=C$,则矩阵$M[A,C]=B$
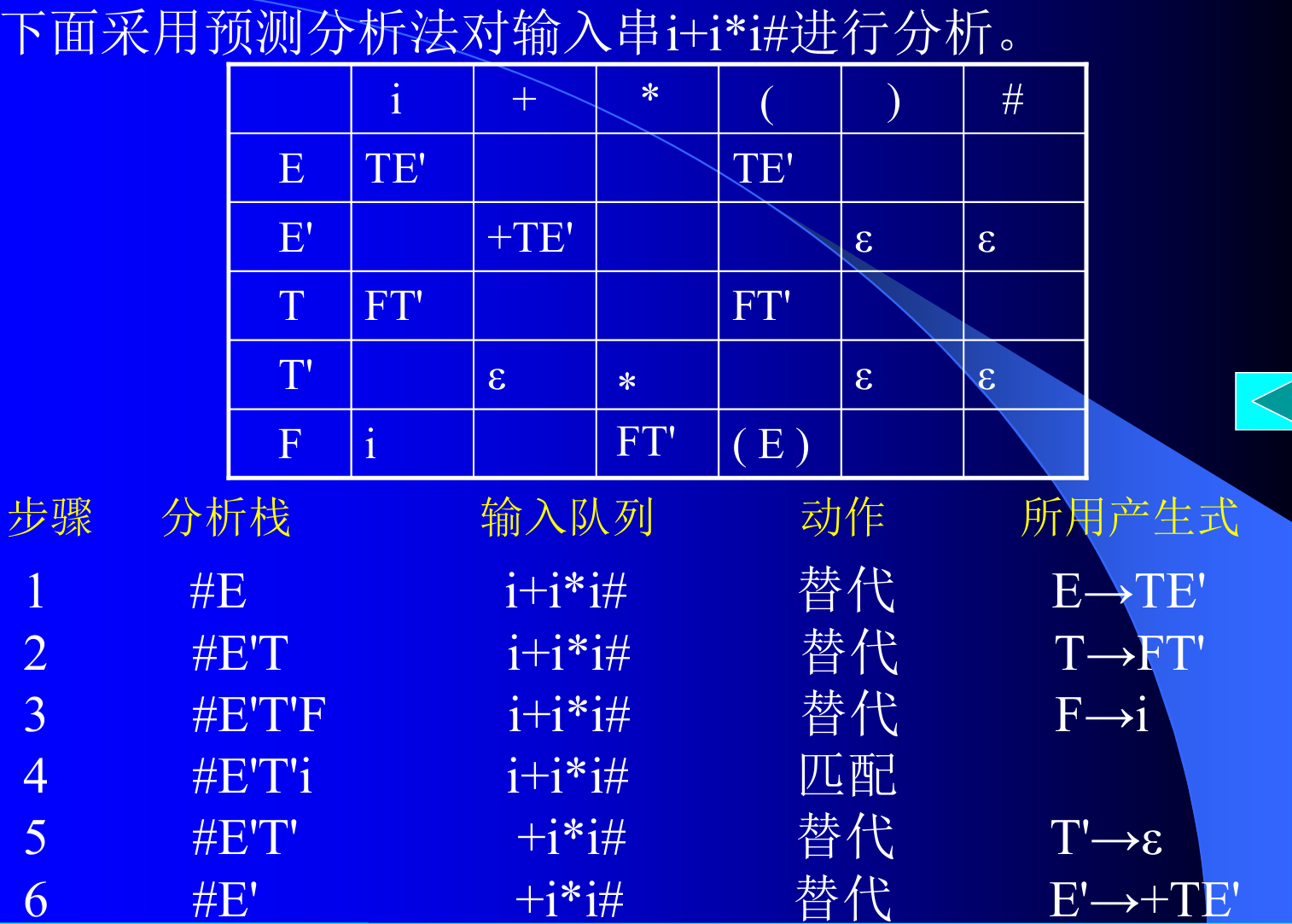
3.分析

4.分析例子