编译原理Ch10

第十章 优化

一、优化

1.概念

• 对程序进行各种等价变换，使得从变换后的程序出发能够生成更有效得目标代码

2.优化的级别

• 局部优化、循环优化、全局优化

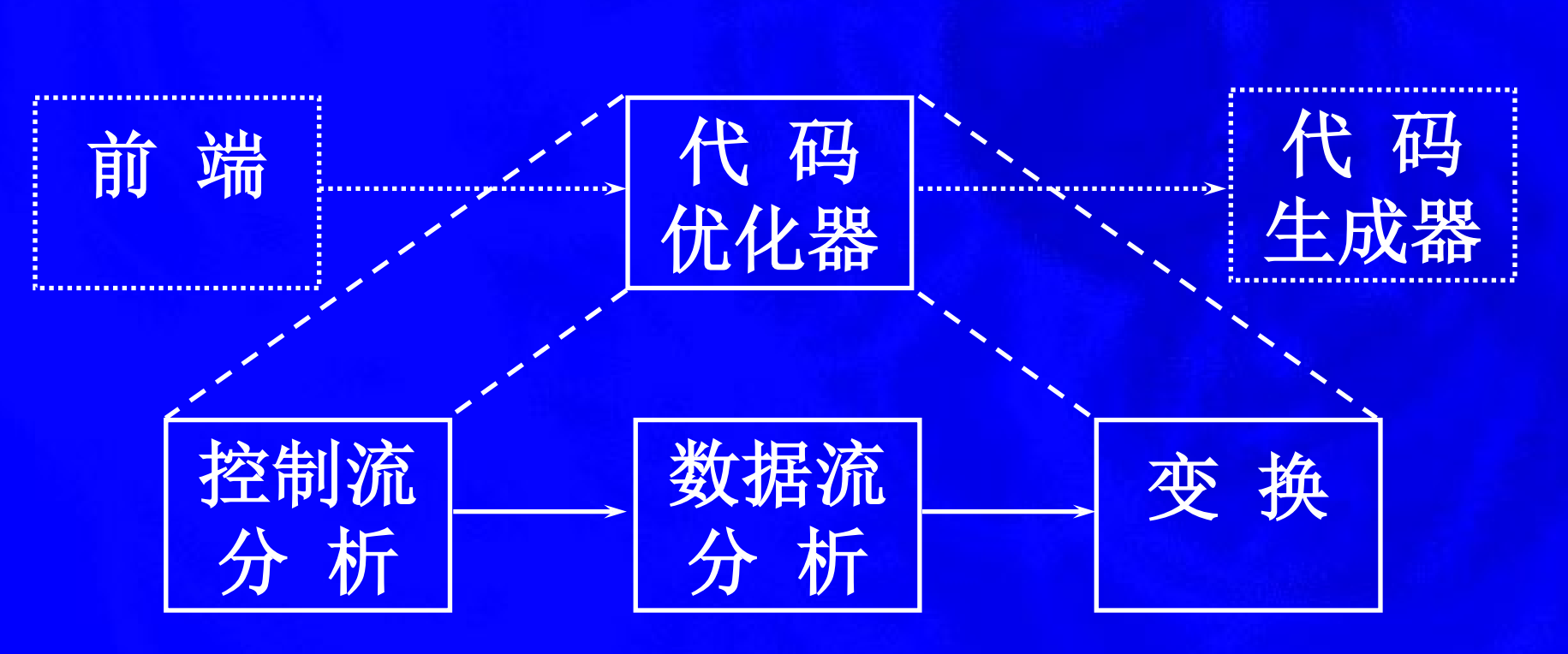
3.优化组成

• 对程序控制流分析
• 数据流分析
• 代码变换
  

4.目的

• 产生更高效的代码

5.遵循的原则

(1)等价原则

• 优化不应改变程序运行的结果

(2)有效原则

• 使优化后所产生的目标代码运行时间较短，占用的存储空间较小

(3)合算原则

• 应尽可能以较低的代价取得较好的优化效果

6.优化的种类

• 删除多余运算（删除公用子表达式）
• 合并已知量
• 复写传播
• 删除无用赋值
• 代码外提
• 强度消弱
• 变换循环控制条件

6.优化示例

(1)源程序

(2)中间代码

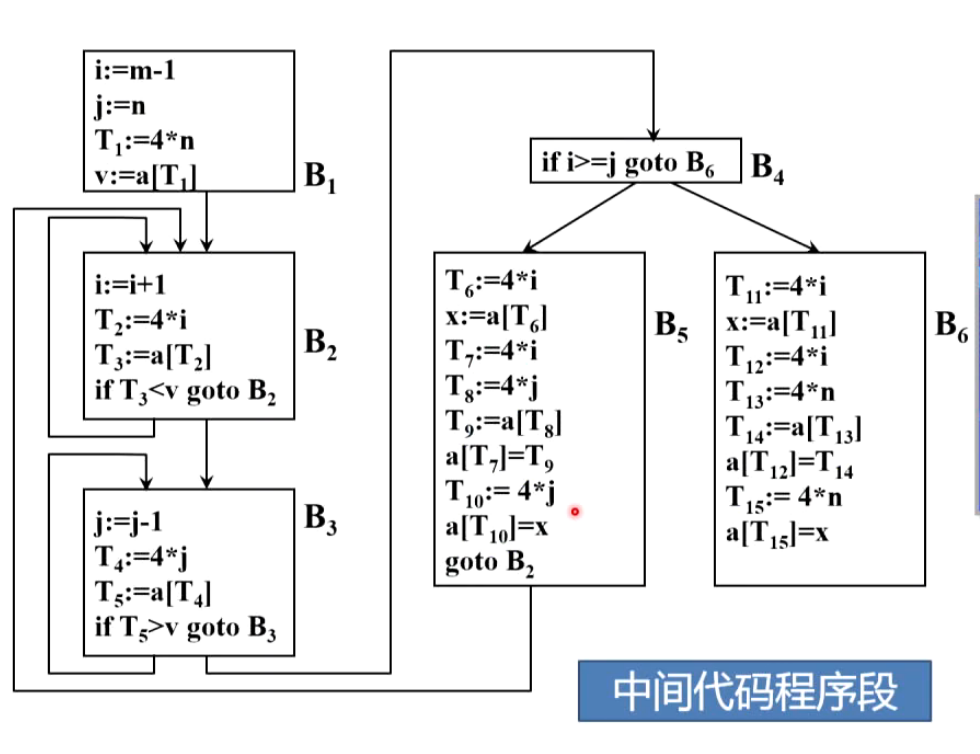
(3)复写传播

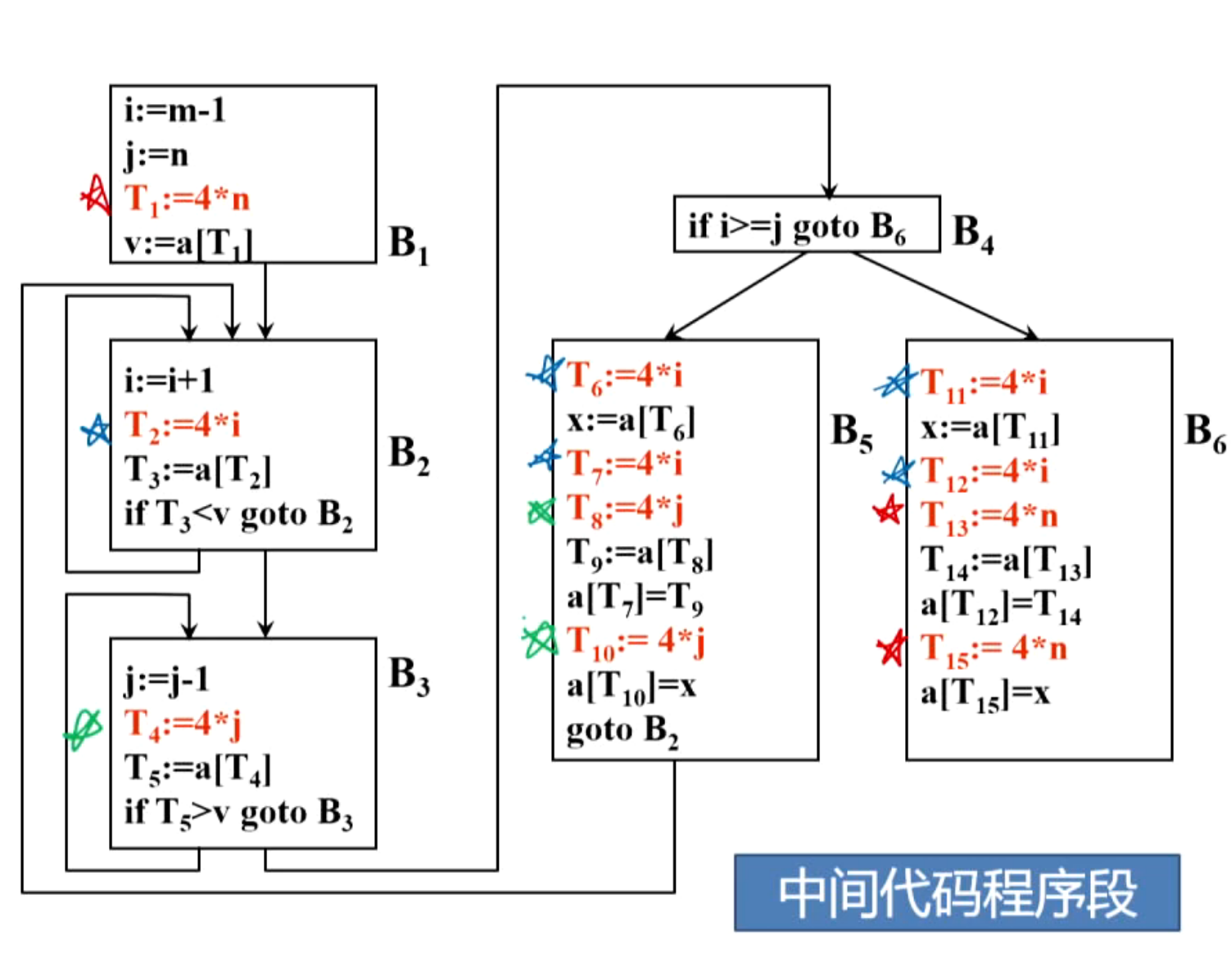
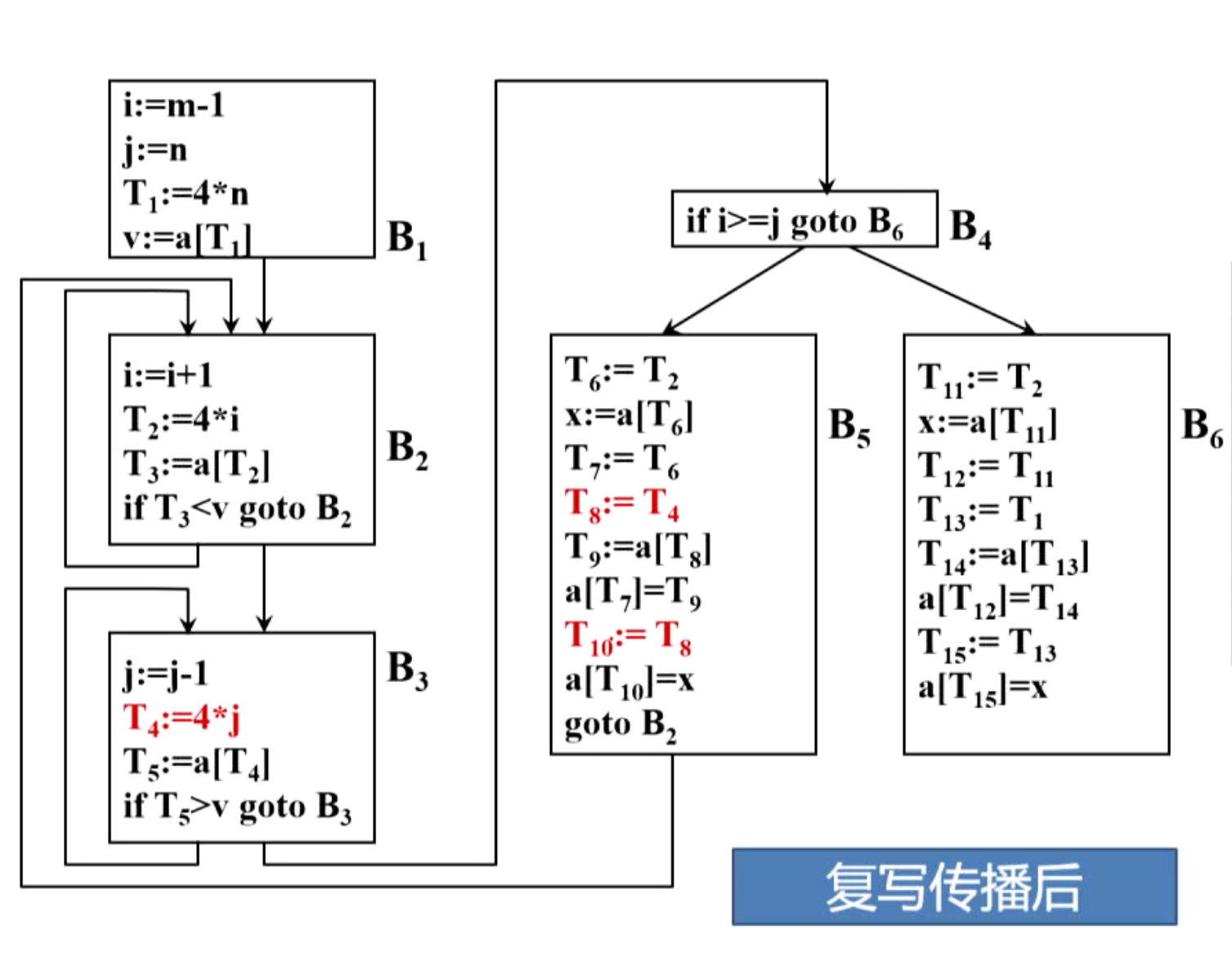
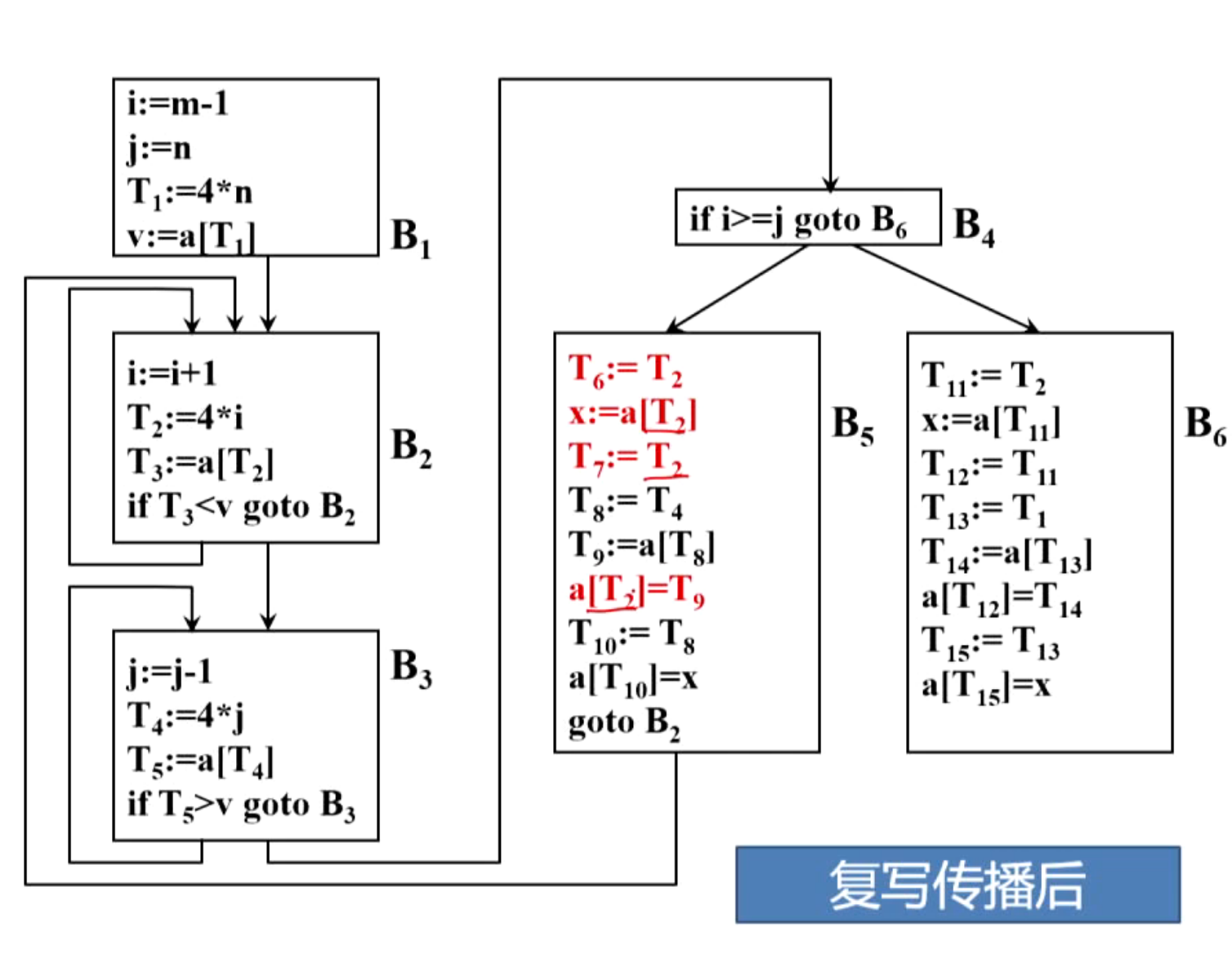
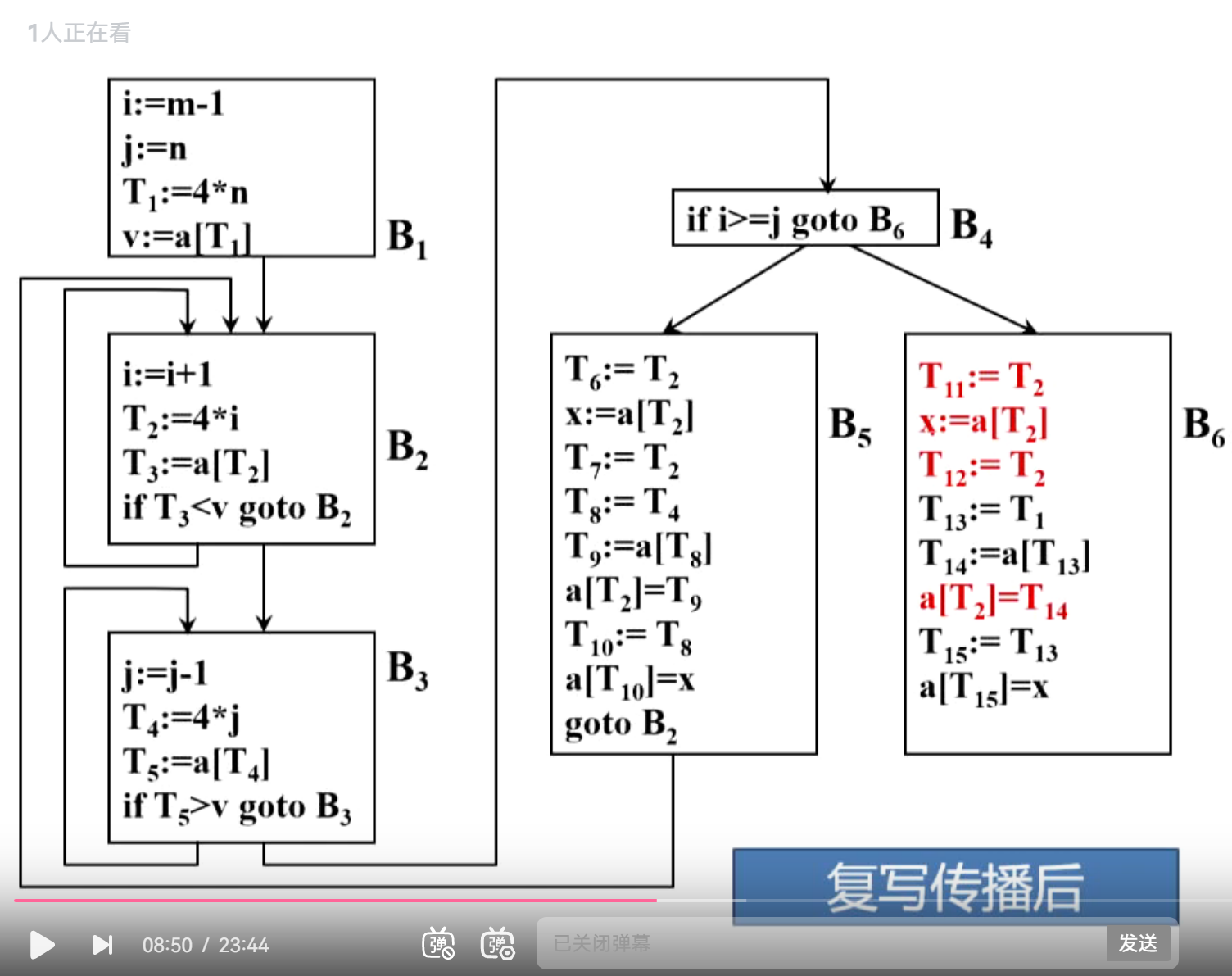
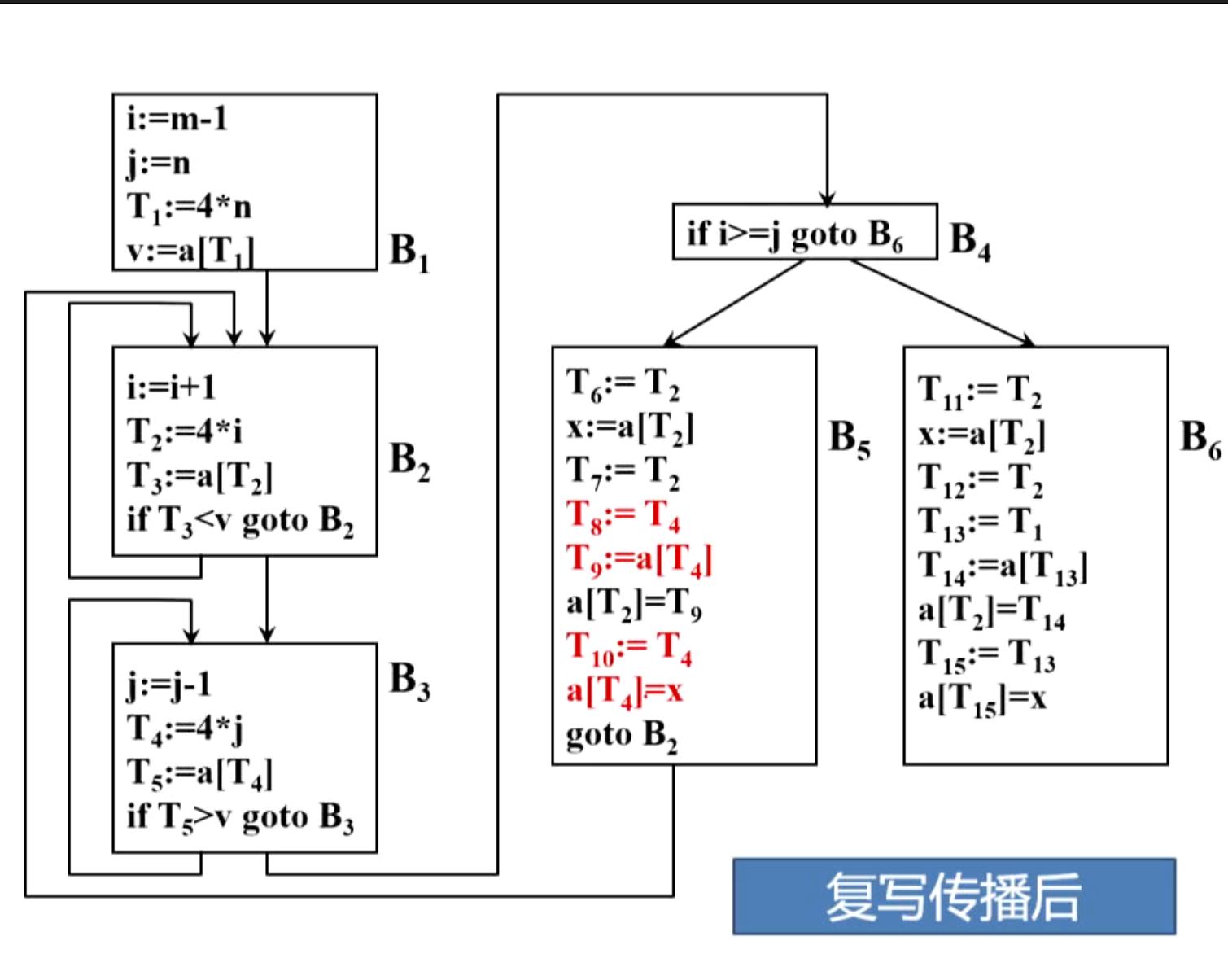
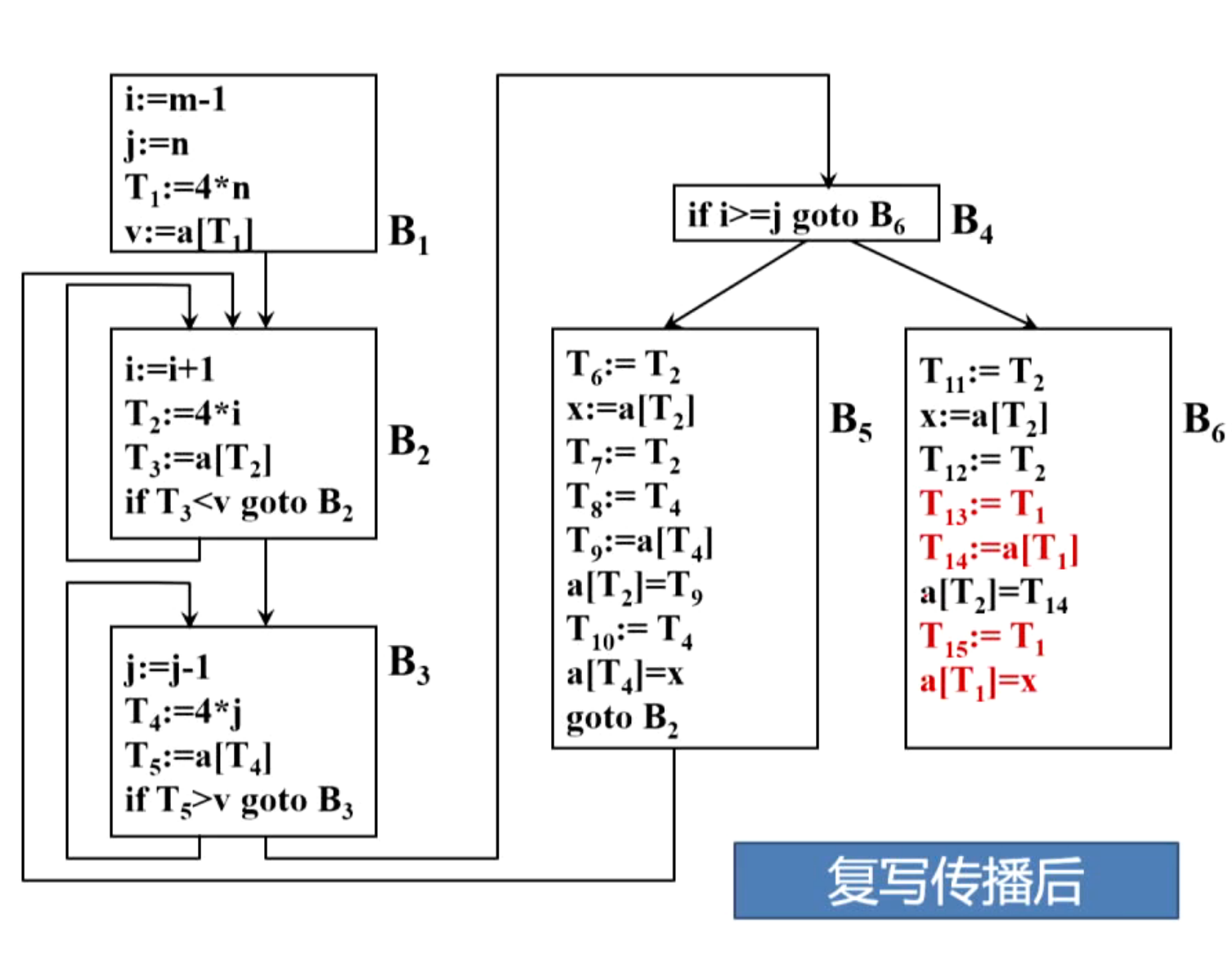
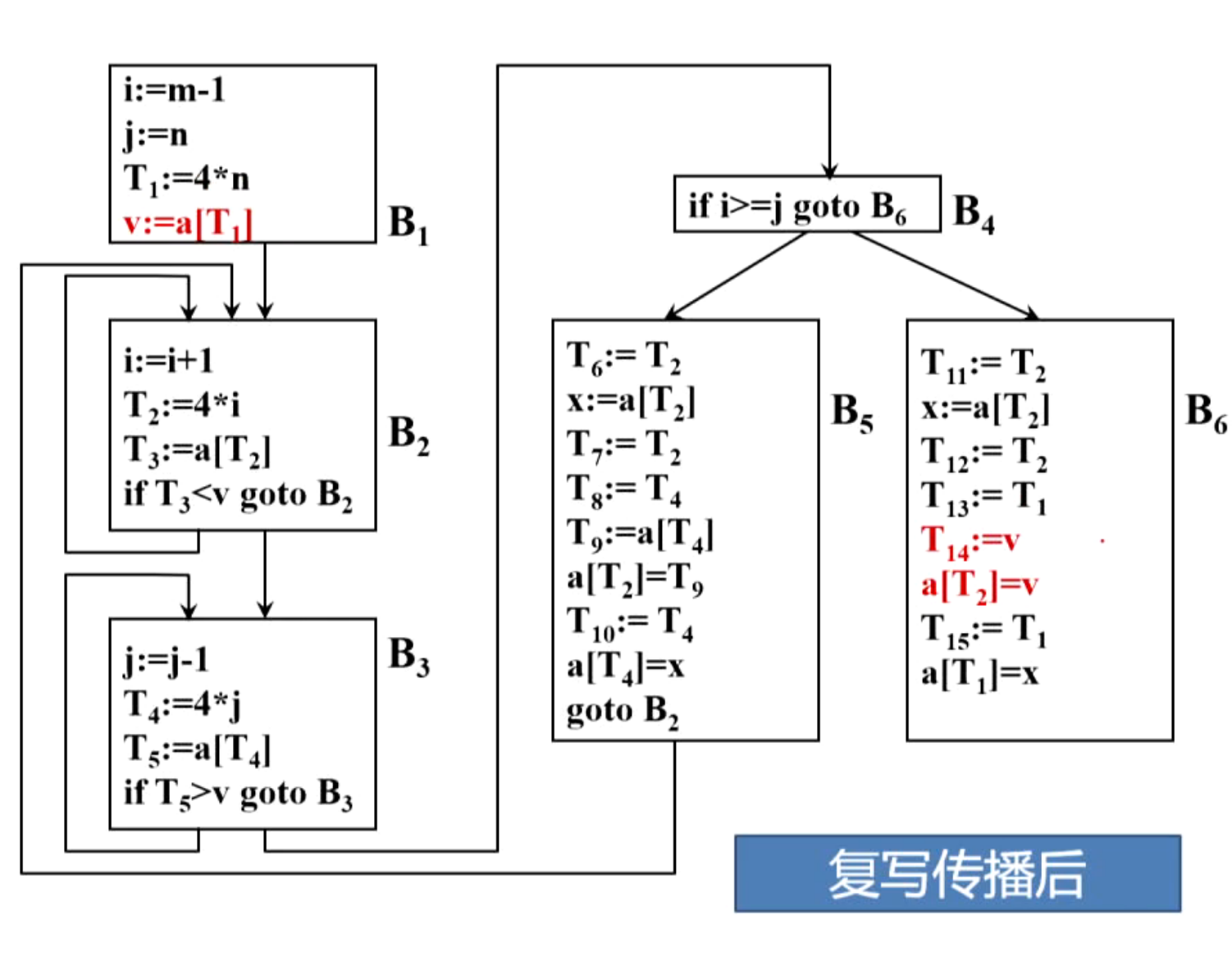
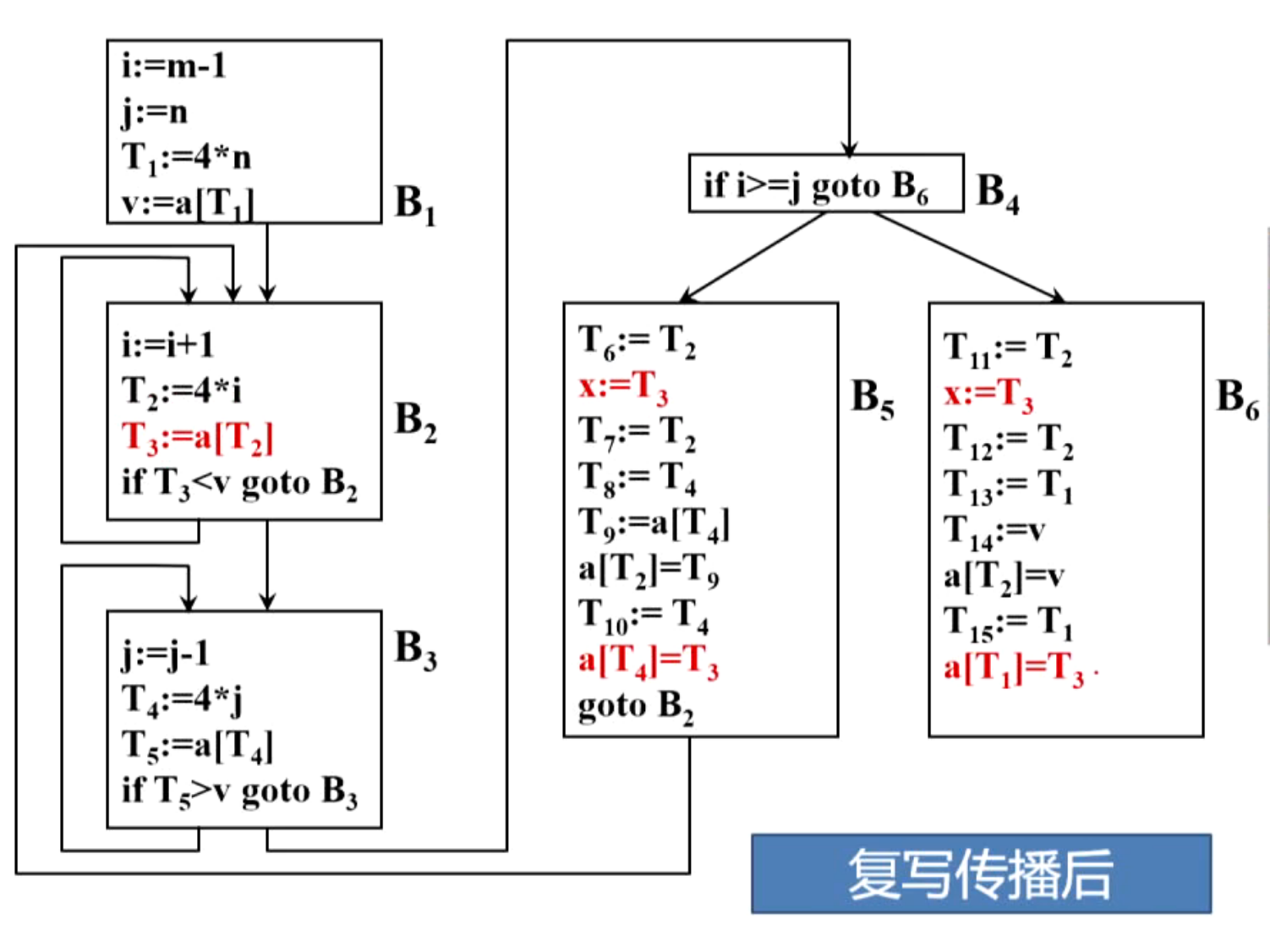
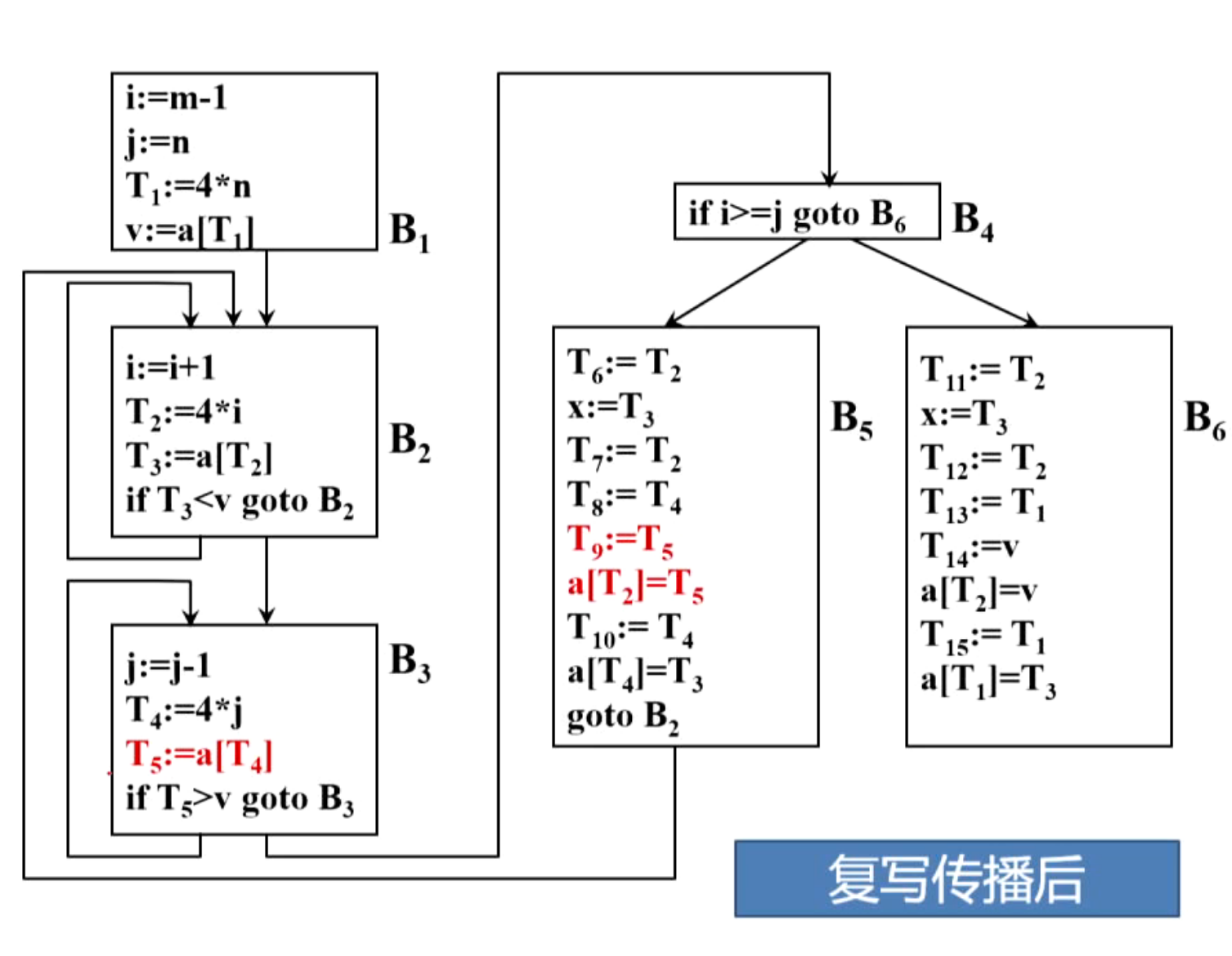
(4)删除无用赋值

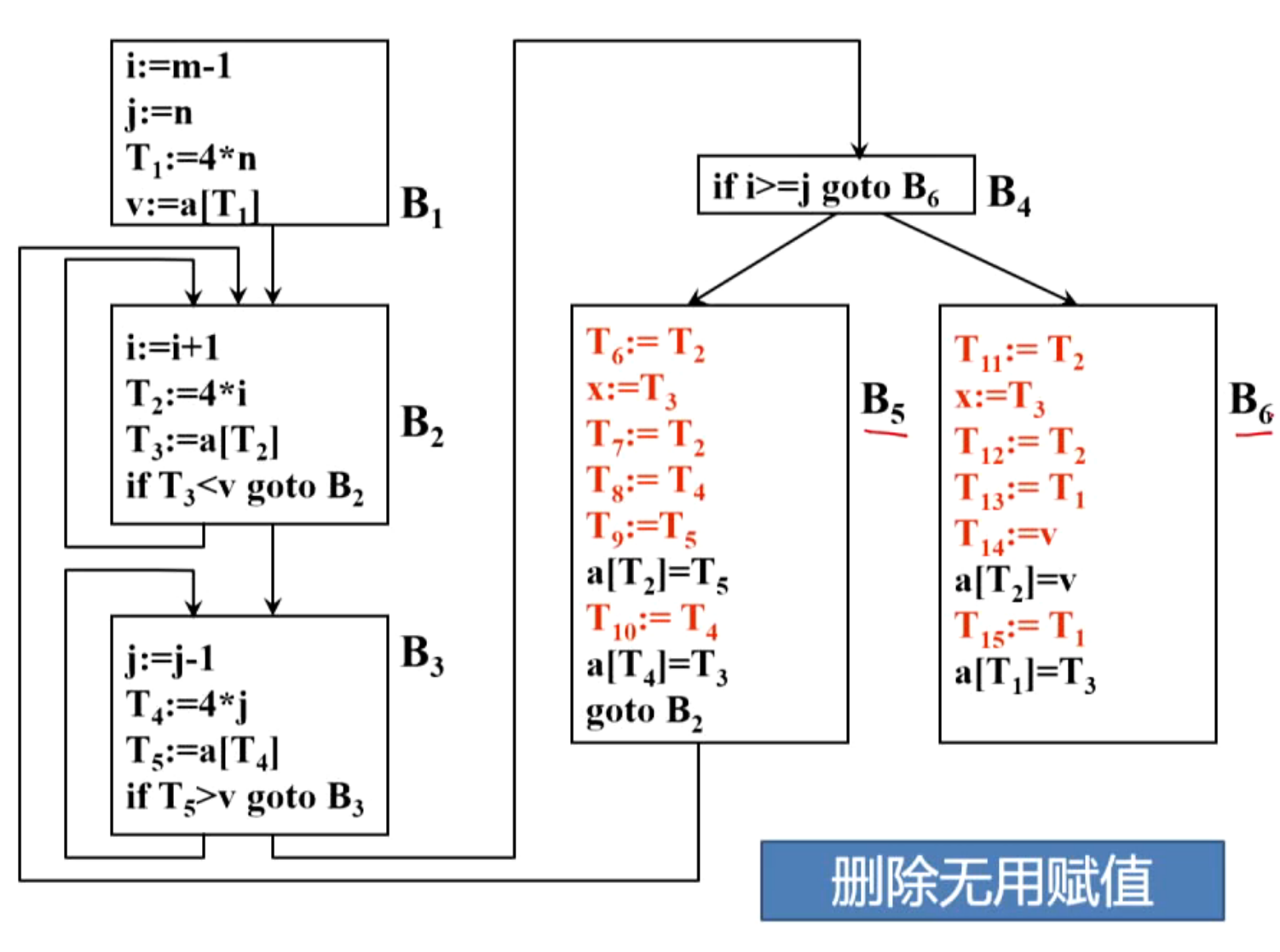
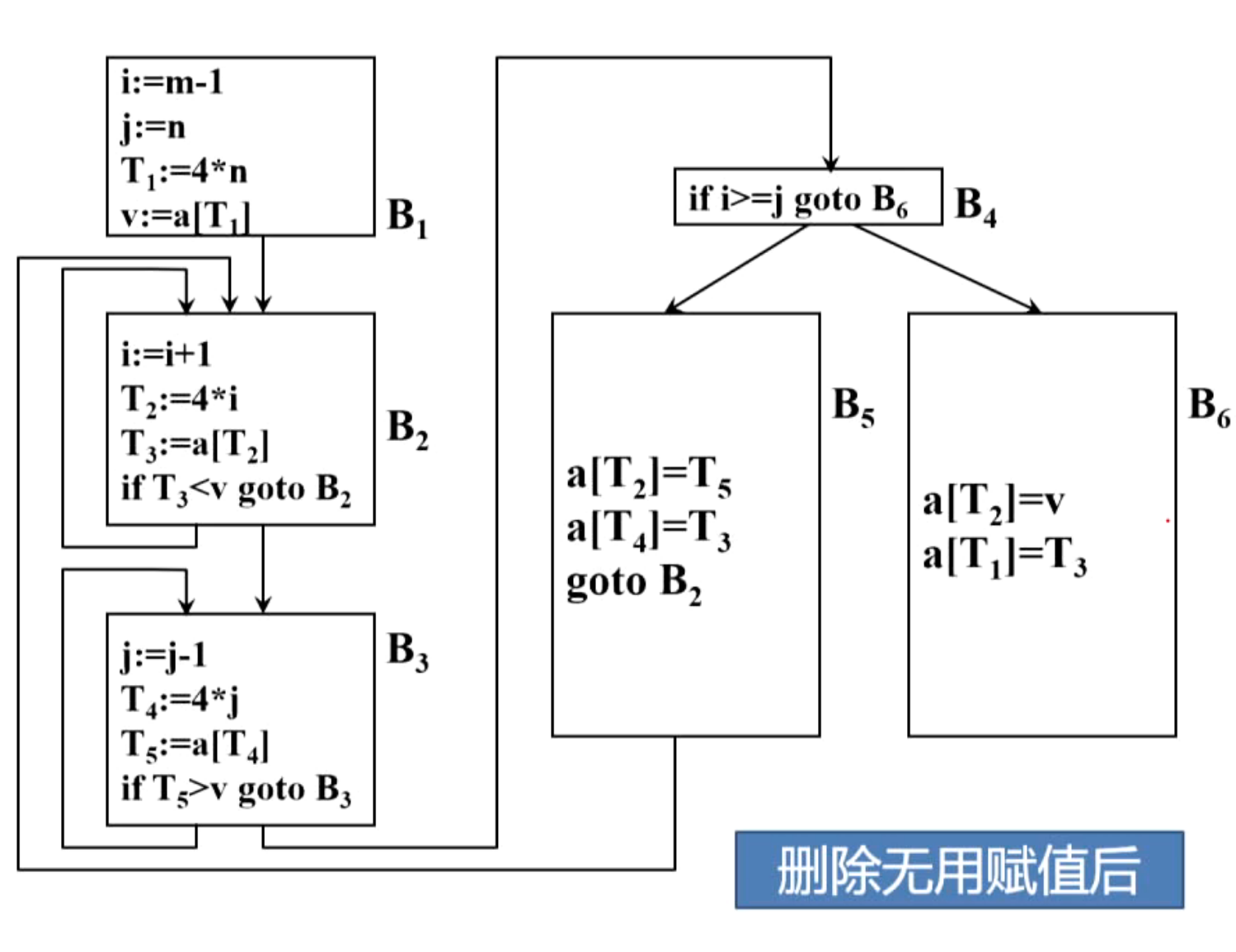
(5)强度削弱

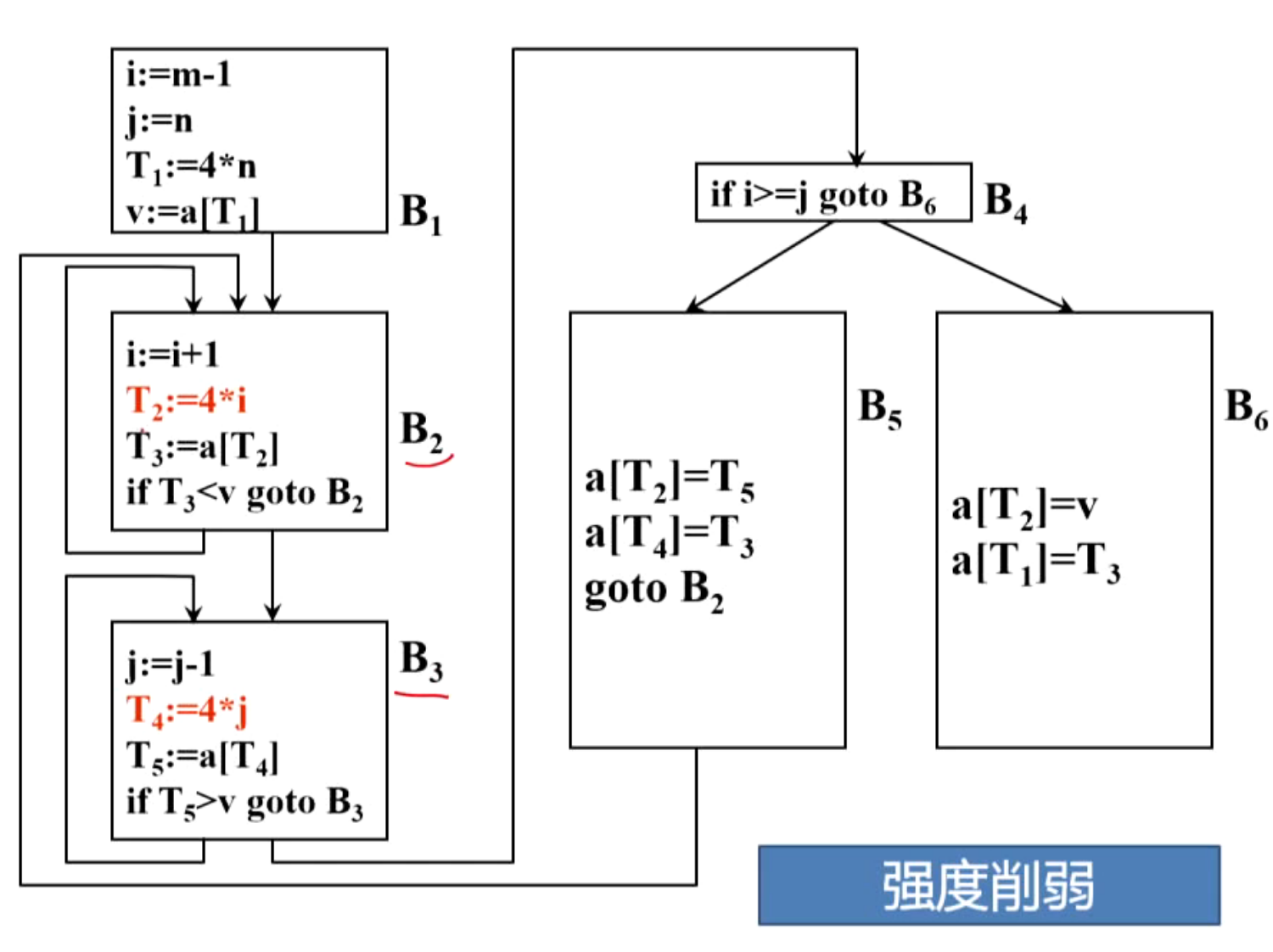
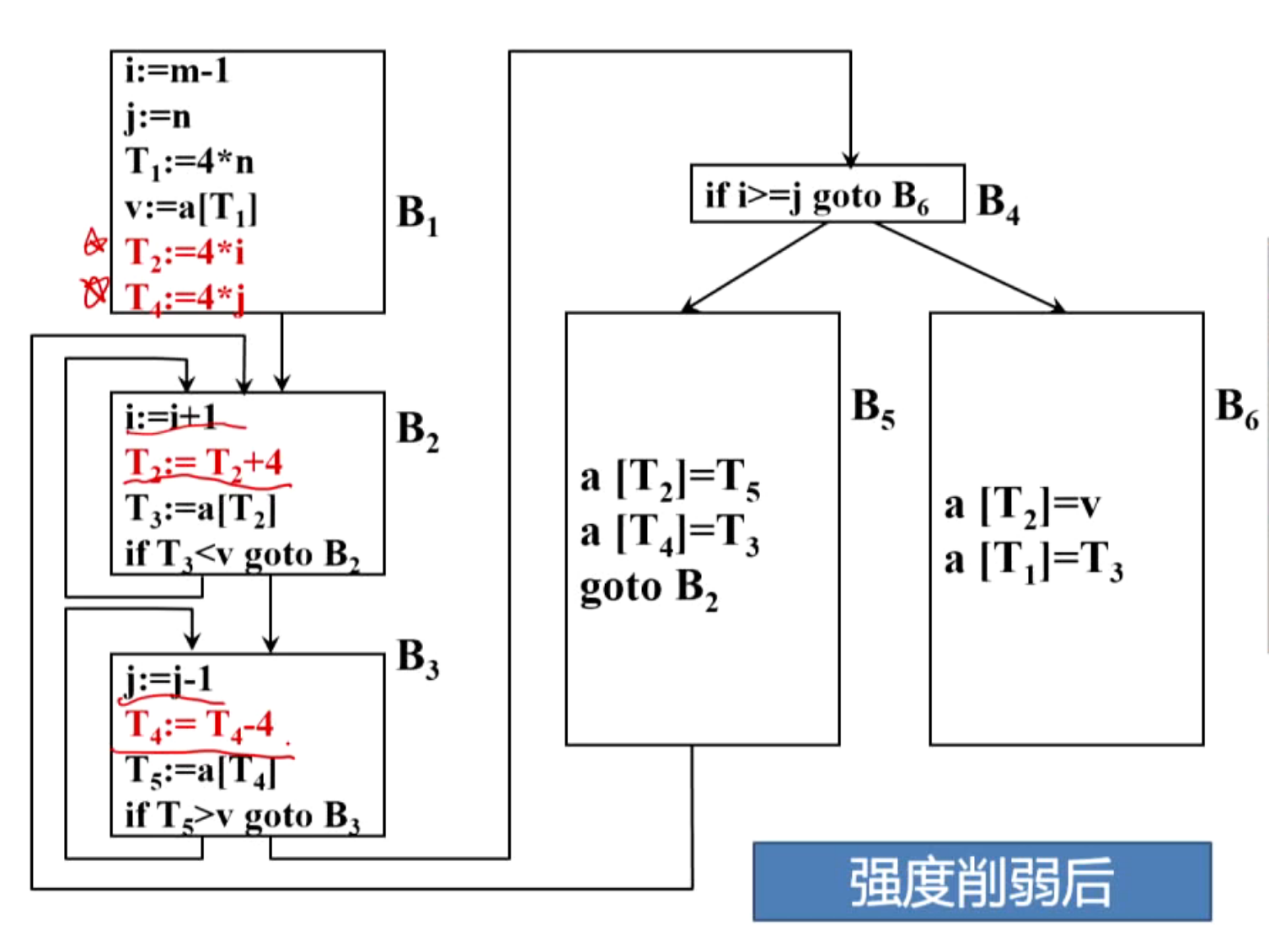
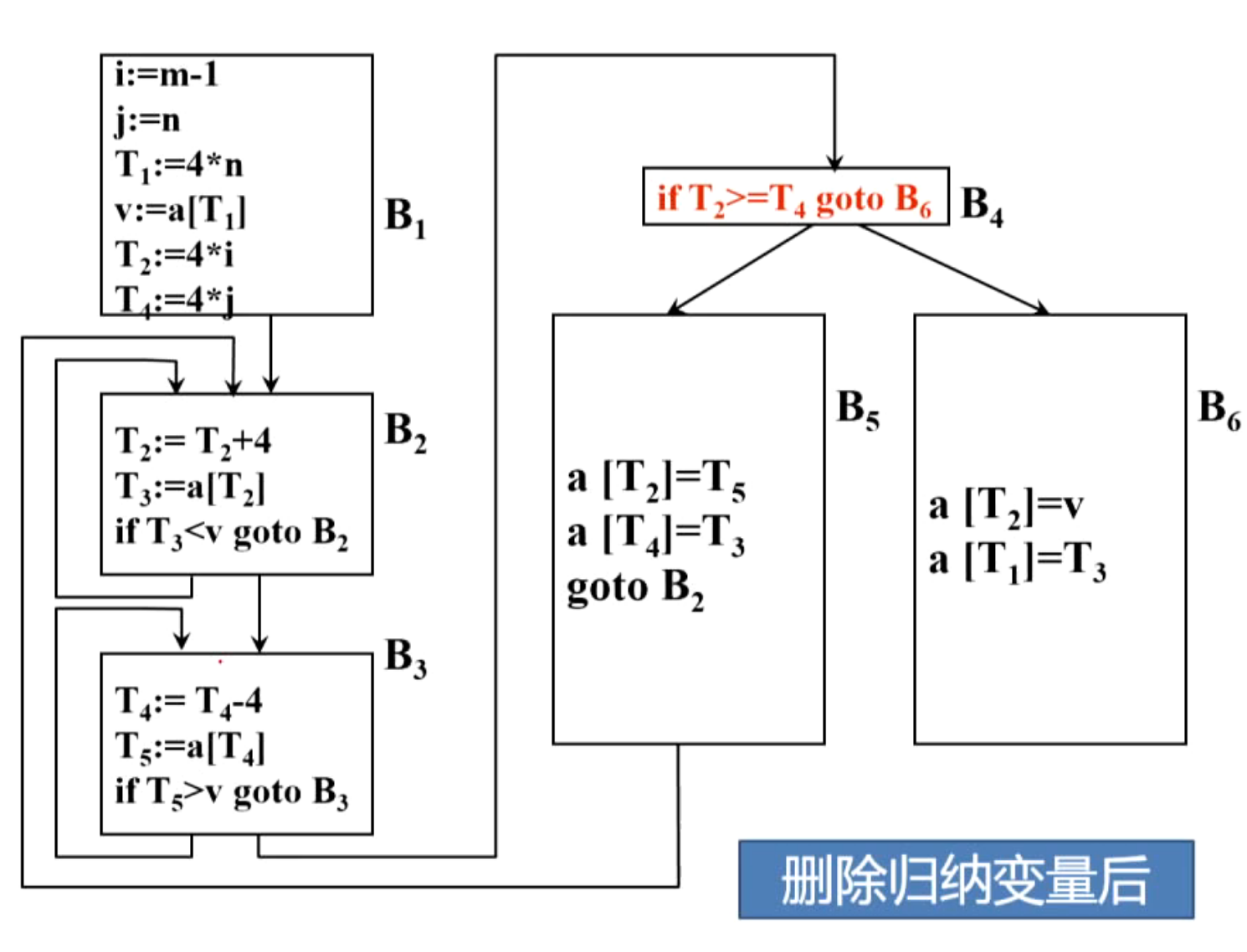
(6)删除归纳变量

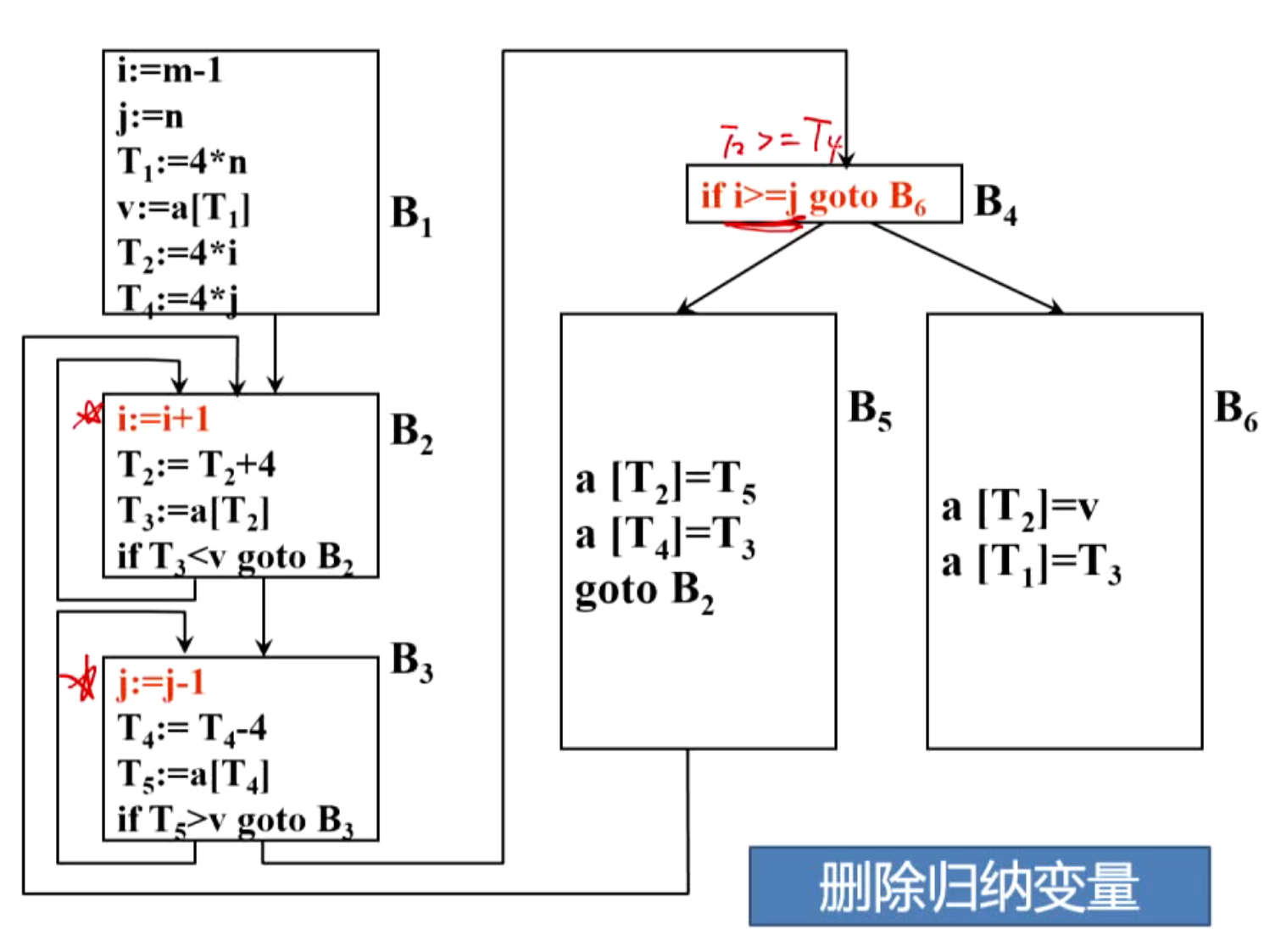
二、局部优化

1.基本快

• 连续的语句序列，控制流从它的开始进入，并从它的末尾离开
• 再用有向边表示基本块之间的控制流信息，就能得到程序的流图

2.划分基本快算法

• 找出中间语言（三地址语句）程序中各个基本快的入口语句
  • 程序的第一个语句
  • 能由条件转移语句或无条件转移语句转移到的语句
  • 紧跟在条件转移后面的语句
• 对以上求出的每个入口语句，确定七所属的基本快。它是由该入口语句到下一入口语句（不包括该入口语句）、或到以转移语句（包括该转移语句）、或一停语句（包括停语句）之间的语句序列组成的

3.流图

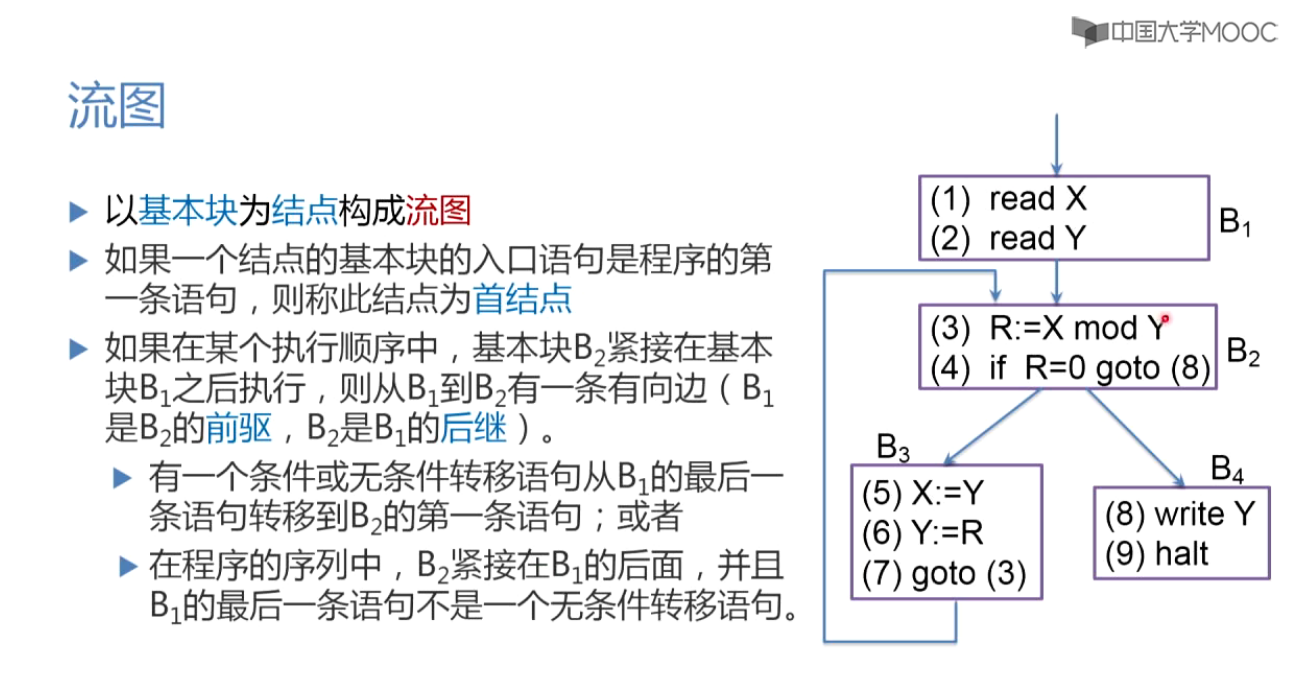
三、有向无环图

1.DAG的扩充

• 在DAG增加标记和附加信息
  • 图的叶节点以一标识符或常数作为标记，表示该结点代表该变量或常数的值
  • 图的内部结点以一运算符作为标记，表示该结点代表应用该运算符对其后继结点所代表的值进行运算的结果
  • 各个结点上可能附加一个或多个标识符（称附加标识符）表示这些变量具有该结点所代表的值

2.四元式的DAG表示

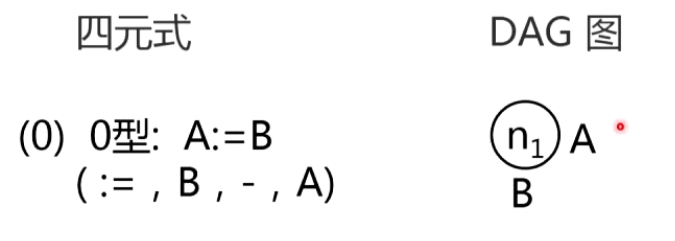
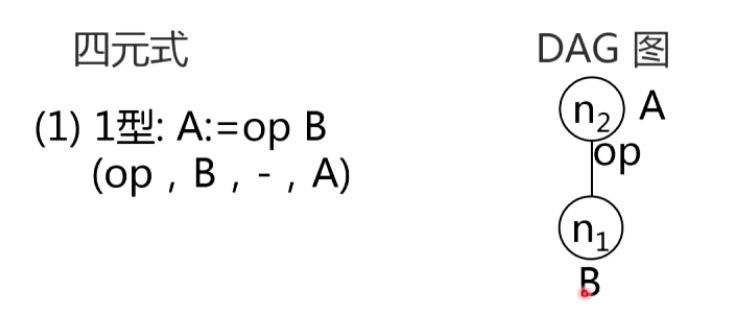
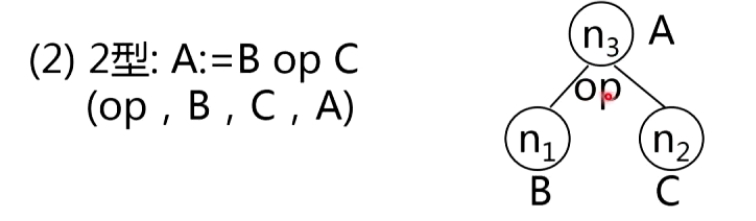
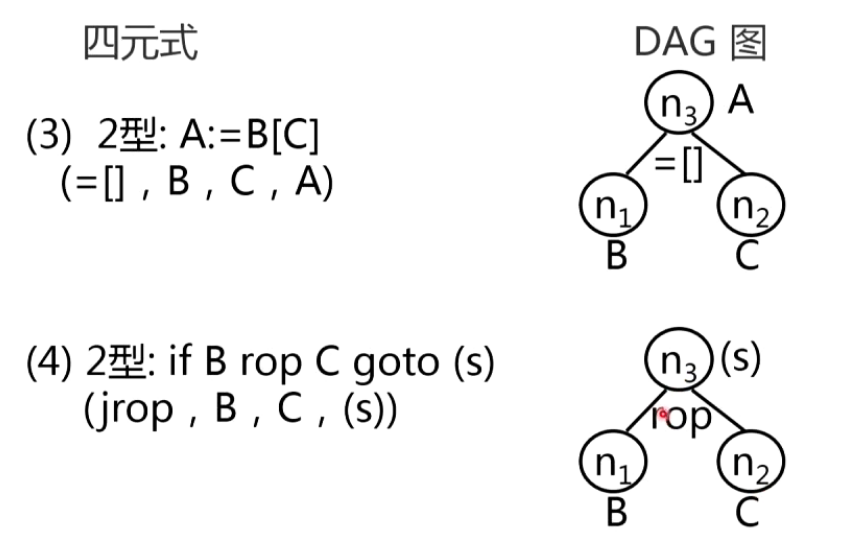
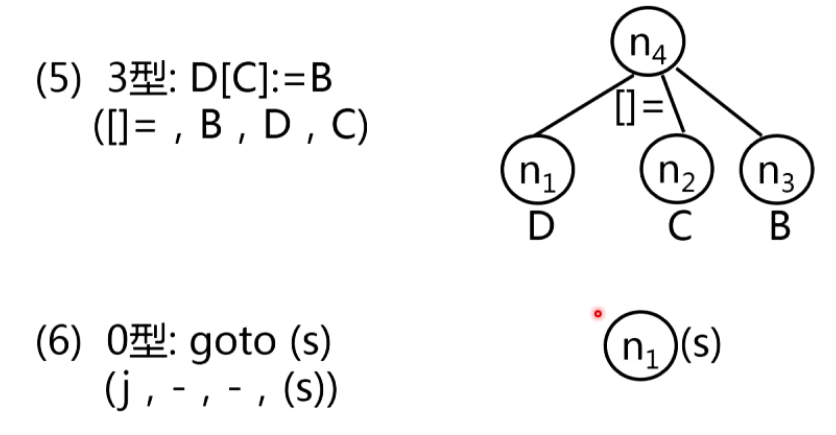
3.基本块的优化算法

• 一个基本块，可用一个DAG表示
• 对基本块中每一条四元式代码，依次构造对应的DAG图，最后基本块中所有四元式构造出来DAG连成整个基本块的DAG
  • 准备操作数的结点
  • 合并已知量
  • 删除公共子表达式
  • 删除无用赋值

4.构造基本块的DAG示例

点击跳转

5.构造基本块的DAG的算法

• 引入函数Node
  

(1)准备操作数结点

• 如果Node(B)无定义，则构造一标记为B的叶节点并定义Node(B)为这个结点
  • 如果当前四元式是0型（A:=B），则记Node(B)的值为n，转4
  • 如果当前四元式是1型（A:=op B），则转2(1)
  • 如果当前四元式是2型（A:=B op C），则(i)如果Node(C)无定义，则构造一标记为C的叶节点并定义Node(C)为这个结点;(ii)转2(2)

(2)合并已知量

• 如果Node(B)是标记为常熟的叶节点，则转2(3);否则，转3(1)（用来处理1型指令）
• 如果Node(B)和Node(C)都是标记为常数的叶节点，则转2(4);否则，转3(2)（用来处理2型指令）
• 执行op B（即合并已知量）。令得到的新常数为P，如果Node(B)是处理当前四元式时新构造出来的结点，则删除它。如果Node(P)无定义，则构造一用P作标记的叶节点n。置Node(P)=n，转4（用来处理1型指令）
• 执行B op C（即合并已知量）。令得到的新常数为P。如果Node(B)或Node(C)是处理当前四元式时新构造出来的结点，则删除它。如果Node(P)无定义，则构造一用P作标记的叶节点n。置Node(P)=n，转4（用来处理2型指令）

(3)删除公共子表达式

• 检查DAG中是否已有一结点，其唯一后继为Node(B)且标记为op（即公共子表达式）。如果没有，则构造该结点n，否则，把已有的结点作为它的结点并设该节点为n。转4
• 检查DAG中是否已有一结点，其左后继为Node(B)，右后继为Node(C)，且标记为op（即公共子表达式）。如果没有，则构造该结点n，否则，把已有的结点作为它的结点并设该节点为n。转4

(4)删除无用赋值

• 如果Node(A)无定义，则把A附加在结点n上冰令Node(A)=n；否则，先把A从Node(A)结点上的附加标识符集中删除（注意，如果Node(A)是叶节点，则其A标记不删除）。把A附加到新结点n上并置Node(A)=n。转处理下一四元式

6.从DAG中得到的优化信息

• 在基本快外被定值并在基本快内被引用的所有标识符，就是作为叶子结点上标记的那些标识符
• 在基本块内被定值并且该值在基本块后面可以被引用的所有标识符，就是DAG各结点上的那些标记或者附加标识符

四、循环优化

1.循环优化的措施（主要介绍前三种）

• 代码外提
• 强度消弱
• 删除归纳变量（变换循环控制条件）
• 循环展开
• 循环合并

2.代码外提

(1)定值到达

• 所谓变量A在某点d的定值到达另一点u（或称变量A的定值点d到达另一点u），是指：流图中从d有一通路到达u且该通路上没有A的其他定值
• A在d点的定值到达了u
  

(2)循环不变运算

• 对四元式A:=B op C，若B和C是常数，或者到达它们的B和C的定值点都在循环外

(3)查找循环中不变运算的算法

• 依次查看L中各基本块的每个四元式，如果它的每个运算对象或为常数，或者定值点在L外，则将此四元式标记为“不变运算”
• 重复第3步直到没有新的四元式被标为“不变运算”为止
• 一次查看尚未标记为“不变运算”的四元式，如果它的每个运算对象或为常数，或者定值点在L外，或只有一个到达定值点且该点上的四元式已被标记为“不变运算”，则把被查看的四元式标记为“不变运算”

(4)把循环不变运算提到循环体外

(5)代码外提的位置

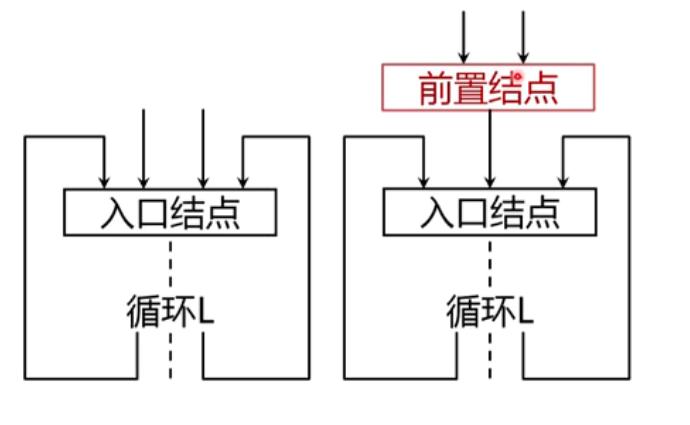
(6)示例

(7)外提的条件

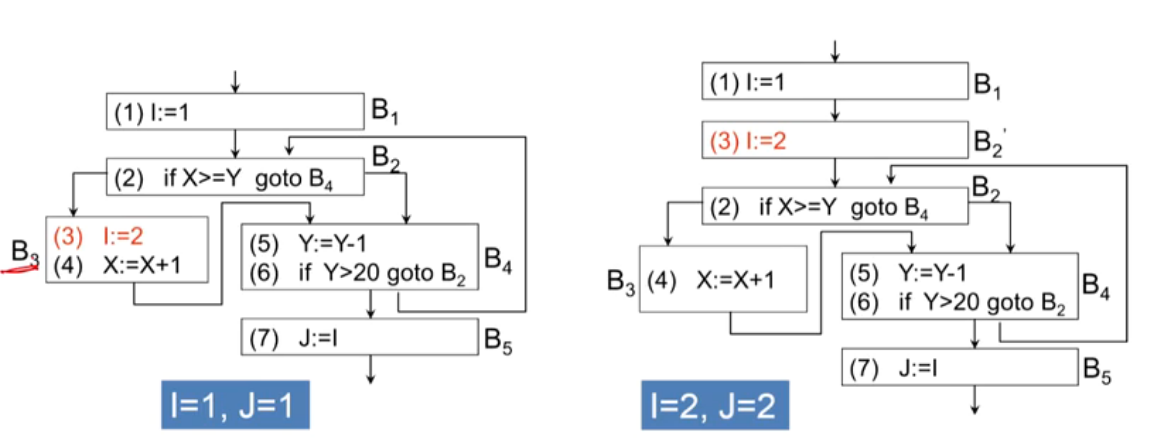
• 出现这种情况是因为$B_3$结点并不是所有循环出口的必经结点
• 因此，必须保证不变运算所在结点是L所有出口结点的必经结点
• 但不变运算所在结点是L所有出口结点的必经结点，也不一定能外提
  
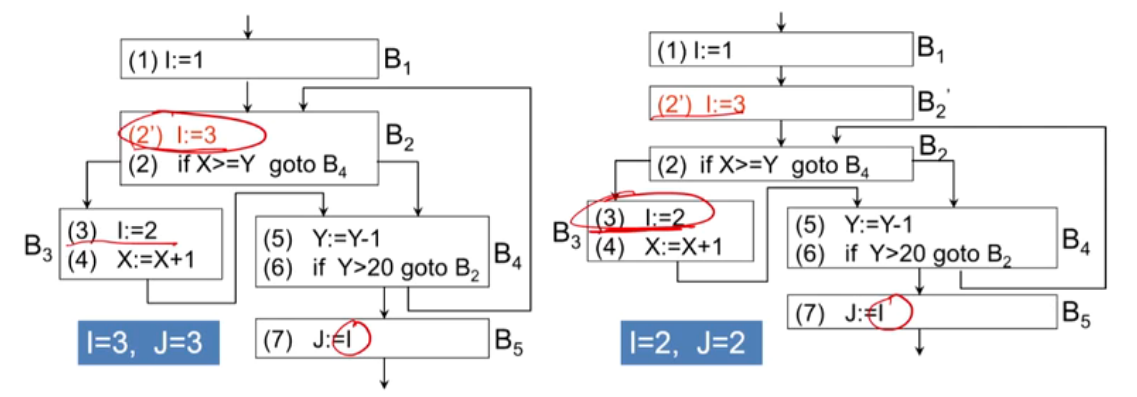
• A在循环中其他地方未再定值，才能把循环不变运算A:=B op C外提
• 但不变运算所在结点是L所有出口结点的必经结点，且A在循环中其他地方未再定值，也不一定能外提
  
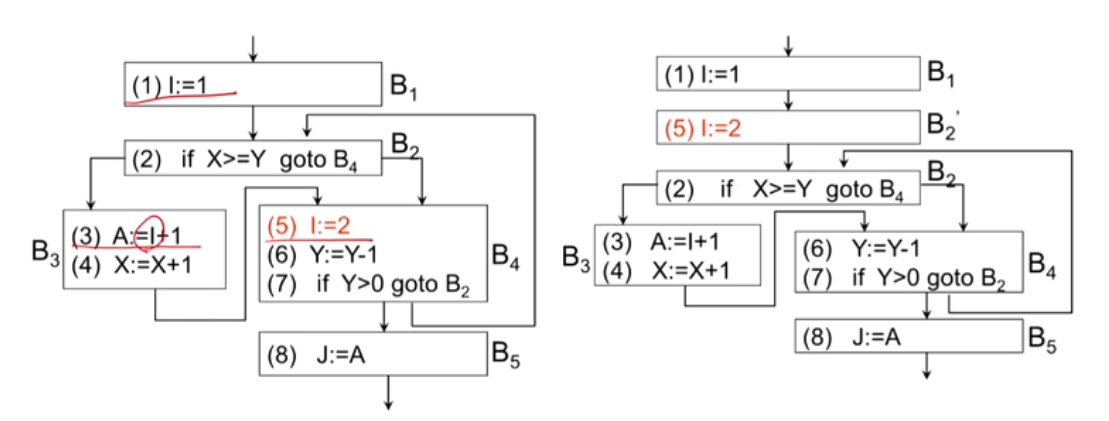
• 此例中，$B_3$中的I不仅可能来自于$B_4$中的I，还有可能来自于$B_1$中的I
• 循环中所有A的引用点只有S中的A的定值才能到达，此例中，要想将(5)外提，则对I的引用点(3)不能再有其他定值(1)到达
• 或者：（2.3相同，1不同）
  • A在离开L后不再是活跃的
  • A在L中其他地方未再定值
  • L中所有A的引用点只有S中的A的定值才能到达

(8)代码外提算法

• 求出L的所有不变运算
• 对于每个不变运算S:A:=B op C 或A:=op B或A:=B检查是否满足上述条件中的一个
• 按步骤1所找出的不变运算的次序，依次把符合步骤2的条件的不变运算S提到L的前置结点中。但是，如果S的运算对象B或C是在L中定值的，那么，只有当这些定值四元式都已外提，才能把S也外提。即将A依赖的B和C的所有定值运算都外提后才能外提A

3.强度消弱

(1)示例

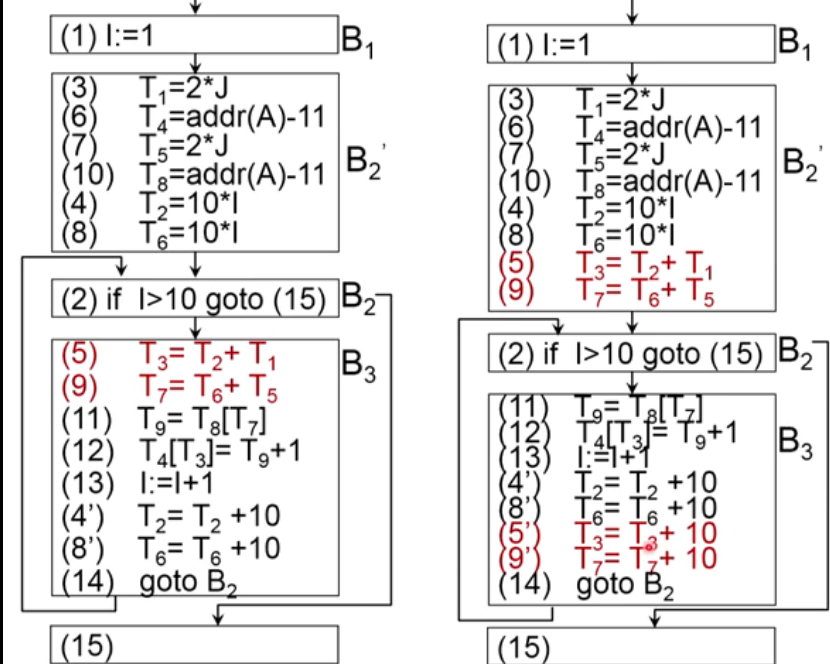
(2)强度消弱

• 强度消弱通常是针对与循环控制变量有线性关系的变量赋值进行
• 经过强度消弱后，循环中可能出现一些新的无用赋值
• 对于消弱下标变量地址计算的强度非常有效

(3)删除归纳变量

• 如果循环中对于变量I只有唯一的形如I:=I±C的赋值，且C为循环不变量，则称I为循环中的基本归纳变量
• 若I是循环中的一个基本归纳变量，J在循环中的定值总是可化归为I的同一线性函数，即J是I的一次函数，则J是归纳变量，并称J与I同族。基本归纳变量也是一归纳变量
  
  
• 删除归纳变量在强度消弱以后进行

(4)强度削弱和删除归纳变量的统一算法框架

• 利用循环不变运算信息，找出循环中的所有基本归纳变量
• 找出所有其他归纳变量A，并找出A与已知基本归纳变量X的同族线性函数关系$F_A(X)$
• 对2中找到的每一个归纳变量A，进行强度消弱
• 删除对归纳变量的无用赋值
• 删除基本归纳变量，如果基本归纳变量B在循环出口后不是活跃的，并且在循环中，除在其自身的递归赋值中被引用外，只在形如if B rop Y goto L的语句中被引用，则可选取一与B同族的归纳变量M来替换B进行条件控制。最后删除循环中对B的递归赋值的代码